
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Логические функции двух переменных
|
|
Имеется 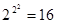 логических функций двух переменных. Определения этих функций, обозначенных от f0 до f15, даны в нижеследующей таблице.
логических функций двух переменных. Определения этих функций, обозначенных от f0 до f15, даны в нижеследующей таблице.
Функции f0 и f15 – конституанты 0 и 1 соответственно.
Функция f3 не зависит от y и равна x (f3(x,y) = x).
Функция f5 не зависит от x и равна y (f5(x,y) = y).
Функция f10 не зависит от x и является отрицанием переменной y (f10(x,y) =  ).
).
Функция f12 не зависит от y и является отрицанием переменной x (f12(x,y) =  ).
).
Оставшиеся функции являются функциями, непосредственно зависящими от двух переменных x и y. Среди них можно выделить наиболее часто употребляемые функции f1 и f7.
| x | ||||
| y | ||||
| f0 | ||||
| f1 | ||||
| f2 | ||||
| f3 | ||||
| f4 | ||||
| f5 | ||||
| f6 | ||||
| f7 | ||||
| f8 | ||||
| f9 | ||||
| f10 | ||||
| f11 | ||||
| f12 | ||||
| f13 | ||||
| f14 | ||||
| f15 |
Функция f1 принимает истинное значение (значение 1), если и только если оба аргумента одновременно являются истинными (x=1 и y=1). Ее называют “конъюнкция”, или же “ функция логического умножения ”, или же “ функция И ” и обозначают обычно как f(x,y) = xy.
Функция f7 принимает значение 1, если хотя бы один из аргументов x = 1 или y = 1. Ее называют “ дизъюнкция”, или же “функция логического сложения”, или же “ функция ИЛИ ” и обозначают обычно как f7(x,y) = x + y.
Функция f6(x,y) =  Это функция “ исключающее ИЛИ ” (f6(x,y) = 1, если x = 1 или y = 1, но не одновременно). Еще ее называют “ сумма по модулю 2 ”, или же “ функция несовпадения ”. Операция, которая соответствует этой функции, часто обозначается в виде
Это функция “ исключающее ИЛИ ” (f6(x,y) = 1, если x = 1 или y = 1, но не одновременно). Еще ее называют “ сумма по модулю 2 ”, или же “ функция несовпадения ”. Операция, которая соответствует этой функции, часто обозначается в виде 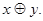
Функция f9(x,y) =  Это функция “ логической идентичности ” или же “ функция совпадения ”. (f9(x,y) = 1, если x и y имеют одинаковые значения). Ее иногда обозначают как
Это функция “ логической идентичности ” или же “ функция совпадения ”. (f9(x,y) = 1, если x и y имеют одинаковые значения). Ее иногда обозначают как  или
или  ~
~  .
.
Функция f8(x,y) =  Это “ функция НИ ” (f8(x,y) = 1, если ни x ни y не равны 1), или же функция “ стрелка Пирса ”, обозначаемая иногда как
Это “ функция НИ ” (f8(x,y) = 1, если ни x ни y не равны 1), или же функция “ стрелка Пирса ”, обозначаемая иногда как  ↑
↑  .
.
Функция f14(x,y) =  Это функция “ логической несовместимости ” (f14(x,y) = 1, если x и y одновременно не равны 1), или же функция “ штрих Шеффера ”, обозначаемая иногда как
Это функция “ логической несовместимости ” (f14(x,y) = 1, если x и y одновременно не равны 1), или же функция “ штрих Шеффера ”, обозначаемая иногда как  /
/  .
.
Функция f2(x,y) = 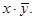 Она называется “ функция запрещения ” (f2(x,y) = 1, если x = 1 и y = 0), иногда обозначаемая как
Она называется “ функция запрещения ” (f2(x,y) = 1, если x = 1 и y = 0), иногда обозначаемая как 
Функция f4(x,y) =  Она называется “ функция запрещения ” (f4(x,y) = 1, если x = 0 и y = 1), иногда обозначаемая как
Она называется “ функция запрещения ” (f4(x,y) = 1, если x = 0 и y = 1), иногда обозначаемая как 
Функция f11(x,y) =  Это функция “ вовлечения ” или “ следования ” (f11(x,y) = 1 для всех комбинаций аргументов, кроме x = 0 и y = 1), обозначаемая иногда как
Это функция “ вовлечения ” или “ следования ” (f11(x,y) = 1 для всех комбинаций аргументов, кроме x = 0 и y = 1), обозначаемая иногда как  или
или 
Функция f13(x,y) =  Это функция “ вовлечения ” или “ следования ” (f13(x,y) = 1 для всех комбинаций аргументов, кроме x = 1 и y = 0), обозначаемая иногда как
Это функция “ вовлечения ” или “ следования ” (f13(x,y) = 1 для всех комбинаций аргументов, кроме x = 1 и y = 0), обозначаемая иногда как  или
или 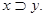
Date: 2015-11-13; view: 520; Нарушение авторских прав