Законы и тождества Булевой алгебры

Можно установить некоторое число теорем, наиболее простые среди которых лежат в основе методов преобразования и упрощения логических выражений.

Логические выражения конструируются на основе ограниченного числа логических переменных x, y, z, …, знаков логических операций отрицания, логического умножения и логического сложения, а также констант 1 b 0. Они носят название логических формул и записываются в виде A(x,y,z,…), B(x,y,z,…), ….Для того, чтобы логические формулы были понятны однозначно, необходимо каждую новую логическую операцию заключать в скобки. В то же время, чтобы сильно не загромождать формулы и свести употребление скобок до минимума, по аналогии с классической алгеброй вводится приоритет выполнения операций: первыми выполняются операции отрицания, затем – логического умножения и, наконец, в последнюю очередь – логического сложения.

Каждая логическая формула может рассматриваться как представление некоторой логической функции переменных x, y, z, …, значение которой для конкретного набора переменных получается без труда заменой значений переменных, которые они принимают для данного набора (0 или 1) в логической формуле и выполняя предусмотренные логические операции.

Для одних и тех же логических переменных можно получить различные логические формулы, среди которых встречаются иногда формулы вида A и B, которые дают одни и те же значения логических функций для всех идентичных наборов логических переменных x, y, z, …, т. е.

A(x,y,z,…) = B(x,y,z,…). (4.1)

Одна из задач Булевой алгебры как раз и состоит в установлении тождества вида (4.1).

Для доказательства тождеств Булевой алгебры достаточно вычислить значения функций слева и справа от знака равенства для всех 2ⁿ комбинаций переменных.

Итак, рассмотрим законы или теоремы Булевой алгебры:

1) Это теорема чистого дуализма. Она выражает для операции отрицания свойство инволюции;

2)

3)

Эти две теоремы выражают свойство коммутативности операций сложения и умножения;

4)

5)

Эти две теоремы выражают свойство ассоциативности операций сложения и умножения;

6)

7)

Первая теорема выражает свойство дистрибутивности умножения по отношению к сложению. Вторая же выражает свойство дистрибутивности сложения по отношению к умножению и не имеет своего эквивалента в классической алгебре;

8)

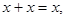
9)

Эти две теоремы также не имеют своих эквивалентов в классической алгебре.

Другие элементарные теоремы:

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

Данные теоремы, в частности, очень полезны при упрощении логических функций.

Общие теоремы:

20)

21)

Это две формы одной теоремы, известной под именем теоремы де Моргана. Она гласит следующее: отрицание логической суммы равно логическому произведению отрицаний и отрицание логического произведения равно логической сумме отрицаний.

Date: 2015-11-13; view: 551; Нарушение авторских прав