Представление чисел в форме с плавающей точкой

Если числа имеют величину различных порядков, то представление с фиксированной точкой ведет к потере информации, т.е. невозможности представления таких чисел. Представление же чисел с плавающей точкой позволяет избежать этих неприятностей. Здесь число представляется следующим образом: N = ± mb^{± E}, где b - основание системы счисления; m - мантисса.

Мантисса представляет значащие цифры числа и записывается в нормализованной форме, чтобы эффективнее использовать разряды, отведенные для ее представления. Обычно мантисса представляется дробным числом, абсолютная часть которого заключена между b^-1 и 1; т.е. 1/b £ m <1. Это число меньше 1, и первая цифра после запятой отлична от нуля, т.е. значащая.

Е называется показателем (порядком). Он представляет (определяет) местоположение десятичной точки в числе, т.е. порядок величины числа, и представляется целым числом.

В ЭВМ число с плавающей точкой представляется отдельно мантиссой (в дробном представлении) и порядком (в целом представлении). Например, в компьютере, обрабатывающем 5-разрядные десятичные числа, число N = 0,0000735287 запишется в виде N = 0,73528^.10^-4 и будет представлено с помощью двух чисел +0,73528 и -4.

Пусть компьютер обрабатывает двоичные числа, в которых n разрядов отведены под мантиссу и p разрядов - под порядок:

Знак мантиссы Знак порядка

¯ 1-й байт 2-й байт 3-й байт ¯ 4-й байт

0 ½1 ½... ½7 ½8 ½... ½15 ½16 ½... ½23 ½24 ½25½... ½31

Мантисса Порядок

Максимально возможное число, представленное в этой разрядной сетке будет иметь мантиссу 1-2^1-n и порядок 2^p-1-1, т.е.»(1-2^1-n)^.2^{2 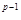-1}» 2^{2 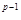-1}. Минимальное же значение мантиссы - 2^-1, а порядок должен быть максимально отрицательным: -2^p-1, тогда минимальное число равно: 2^-1.2^-2 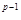= 2^-1-2 .

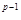Если n = 24 и p= 8, то диапазон представленных чисел по модулю будет от 2^-129 до 2⁺¹²⁷. При выполнении операций с плавающей точкой возникает меньше проблем с переполнением разрядной сетки, чем для операций с фиксированной точкой. Однако операции с плавающей точкой более сложные, так как они требуют нормализации и денормализации мантисс. В самом деле, сложение или вычитание требует денормализации меньшего из двух операндов, для того чтобы выровнять порядки обоих слагаемых. Затем, возможно, потребуется нормализация результата, а деление вызовет денормализацию делимого, если абсолютное значение его мантиссы больше, чем у делителя.

Date: 2015-11-13; view: 387; Нарушение авторских прав