Аналогично определяется действующее значение напряжения: U  0,707Um. Действующие значения токов и напряжений называют еще их среднеквадратичными значениями

⇐ ПредыдущаяСтр 7 из 11Следующая ⇒

Среднее значение гармонического тока:

. (4)

Для гармонического тока I_ср = 0. Этот результат понятен, если учесть, что уравнение определяет площадь, ограниченную кривой i(t) за период Т.

Гармонические колебания можно представить различными способами: функциями времени (временные диаграммы); вращающимися векторами (векторные диаграммы); комплексными числами; амплитудными и фазовыми спектрами. Тот или иной способ представления применяется в зависимости от характера решаемых задач.

1) Временное представление гармонических колебаний наглядно, однако его использование в задачах анализа цепей затруднительно, так как требует проведения громоздких тригонометрических преобразований (иллюстрация).

2) Более удобно векторное представление гармонических колебаний, при котором каждому колебанию ставится в соответствие вращающийся вектор определенной длины с заданной начальной фазой. На рисунке 2а показано векторное представление двух колебаний i₁ и i₂: i₁ = I_m₁sin(wt + j₁); i₂ = I_m₂sin(wt + j₂).

Их сумму i₃ можно найти по формулам суммирования векторов:

i₃ = i₁ + i₂ = I_m3sin(wt + j₃), (5)

где ; .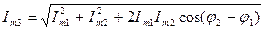

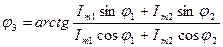Рисунок 2 - Представление гармонических колебаний

Величина j = j₂ - j₁ называется фазовым сдвигом между колебаниями i₁ и i₂.

Совокупность векторов, изображающих гармонические колебания в электрической цепи, называют векторной диаграммой. Векторные диаграммы можно строить как для амплитудных, так и для действующих значений токов и напряжений.

3) Наиболее распространенными являются представления гармонических колебаний с помощью комплексных чисел. Эти представления лежат в основе комплексного метода расчета электрических цепей - метода комплексных амплитуд. Представим ток i на комплексной плоскости. Для этого изобразим вектор I_m на комплексной плоскости с учетом начальной фазы (рисунок 2б). Будем вращать этот вектор в положительном направлении (против часовой стрелки) с угловой частотой.. Тогда в любой момент времени положение вращающегося вектора определится комплексной величиной (комплексным гармоническим колебанием) (иллюстрация):

i(t) = I_me^j⁽^w^t⁺^j⁾ = I_mcos(wt + j_i) + jI_msin(wt + j_i). (6)

Первая часть слагаемого отражает проекцию вращающегося вектора на вещественную ось, а вторая часть - на мнимую ось. Оценив второе слагаемое, приходим к выводу: синусоидальный ток i на комплексной плоскости представляется в форме проекции на мнимую ось вращающегося вектора:

i = Im[I_me^j(^w^{t +}^j⁾] = Im [ 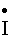_me^j^w^t], (7)

где Im - сокращенное обозначение слова Imaginarins (мнимый);

Величина 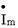носит название комплексной амплитуды тока.

Если гармоническое колебание задается в форме косинусоиды, то на комплексной плоскости этому току соответствует проекция вектора на вещественную ось:

i = Re [I_me^j(^w^{t +}^j⁾] = Re [ 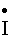_me^j^w^t], (8)

где Re - сокращенное обозначение слова Realis (действительный, вещественный).

Комплексную амплитуду синусоидальной функции заданной частоты можно рассматривать как преобразование временной функции в частотную область.

4) Спектральное (частотное) представление гармонических колебаний состоит в задании амплитудного и фазового спектров колебания

Пример решения 1:

Напряжение u (t) и ток u (t) изменяются по синусоидальному закону (см. рис. 3) с одной частотой, следовательно, мгновенные значения тока и напряжения в цепи записываются:

u = U_m sin(w t+ y _u),

i = I_m sin(w t+ y _i),

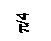
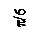
где U_m – амплитудное значение напряжения; I_m – амплитудное значение тока; w = 2p f – угловая частота; f = 1/ T – частота синусоидальных напряжения и тока; Т – период; y _u –- начальная фаза синусоидального напряжения; y _i – начальная фаза синусоидального тока

w = 2p f= 2p×50= 314 рад/с; y _u = -p/6 = -30 ^о; y _i = p/4 = 45^о

Начальная фаза напряжения y _u имеет знак (-), так как синусоида u (t) сдвинута по оси абсцисс вправо от начала координат (величина самой функции при t =0 имеет отрицательное значение). Напомним, что началом любой синусоиды полагается точка перехода функции из отрицательного значения в положительное значение. Поэтому же начальная фаза тока имеет знак (+), так как синусоида i (t) сдвинута по оси абсцисс влево от начала координат. Таким образом, в соответствии с (3.1) и (3.2) имеем:

u = 141×sin (314 t – 30 ^о) В, i = 2,82×sin (314 t + 45 ^о) А.

Синусоидальные функции времени изображаются также комплексными числами, которые, по сути, аналитически описывают вращающиеся радиус-векторы на комплексной плоскости, рассматриваемые в момент времени t =0.

Комплексные изображения синусоидальных величин чаще всего записываются для действующих значений. Поэтому в первую очередь определим действующие значения тока и напряжения данной цепи:

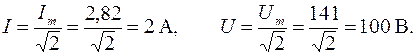
Представим u (t) и i (t) в комплексной форме (показательная форма записи комплексных чисел):

, .

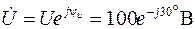Модуль комплексного напряжения равен действующему значению напряжения U участка цепи, а аргумент – начальной фазе (начальная фаза синусоидального напряжения y _u)и, соответственно, модуль комплексного тока равен действующему значению тока I участка цепи, а аргумент – начальной фазе (начальная фаза синусоидального напряжения y _i). Напомним, что такое представление возможно, поскольку ток и напряжения изменяются с одной и той же угловой частотой и, следовательно, изображающие их векторы на комплексной плоскости взаимно неподвижны.

Определим полное комплексное сопротивление цепи

Z = Z e ^j ^j = / 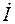= Ue ^j ^y ^u / Ie ^j ^y ⁱ = (100e ^- ^j ³⁰^o ) / (2e ^j ⁴⁵^o ) =

= (100 /2) e ^j ^(-30^o^{- 45}^o⁾ = 50 e ^– ^j ⁷⁵^oОм,

где Z – полное сопротивление цепи, Ом; j – разность фаз между током и напряжением (угол сдвига фаз), j < 0.

В алгебраической форме записи комплексное сопротивление цепи Z имеет вид (переход осуществляется с помощью формулы Эйлера):

Z = Ze ^j ^j =Z cosj +j Zsinj = R+j X =

= 50cos (-75 °) + j 50sin (-75°) =12,94 – j 48,3 Ом.

Здесь R – действительная часть (активное сопротивление), а Х – мнимая часть (реактивное сопротивление) комплексного сопротивления цепи Z.

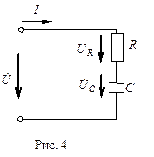
Схема замещения цепи (рис. 4) представляется последовательным соединением резистивного элемента R и емкости С, так как мнимая часть X комплексного сопротивления цепи имеет отрицательный знак. Цепь носит “емкостной” характер. Об этом также свидетельствует отрицательный знак угла сдвига фаз. Ток опережает напряжение по фазе.

Пример решения 2:

Схема замещения реальной индуктивной катушки (рис. 3.3) содержит соединенные последовательно элементы R _К и L _К.

Полное комплексное сопротивление цепи индуктивной катушки в алгебраической форме записи

Z _К= R _К +j X _К = 3+ j 4 Ом, (3.3)

где X _К= X_L=L= 2 fL - индуктивное сопротивление,Ом;

X_К=  L_К= 2 f L _К= 2 × ×0,0127 = 3,99»4 Ом.

На рис. 5 представлен треугольник сопротивлений, построенный в соответствии с формулой (3.3).

В показательной форме комплексное сопротивление цепи индуктивной катушки запишется Z _К= Z _К e ^j ^jОм.

Из простых геометрических соображений очевидно:

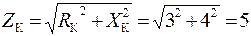Ом; 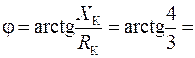53,13°»53°,

где Z _К–полное сопротивление цепи; j- разность фаз между током и напряжением, следовательно Z _К = 5 e ^j ⁵³^°Ом.

Так как  >0 (+53°), то, как и все положительные углы, он откладывается от оси вещественных чисел против часовой стрелки. (рис. 6)

Варианты заданий к самостоятельной работе

Таблица 1

Параметры Вариант

U_m, В 14,1 28,2 42,3 56,4 84,6 98,7

I_m, А 5,64 0,846 42,3 1,41 0,564 0,987 5,64 4,23

Т, с 0,01 0,02 0,04 0,0025 0,025 0,02 0,01 0,0025

y _u, рад -p /4 p /6 p /2 p /10 p /9 -p /8 -p /4 -p /8

y, рад p /8 -p /4 p /8 -p /8 -p /5 p /7 -p /6 p /10

Таблица 2

Параметры Вариант

R_к, Ом

L_к, Гн 0,00478 0,0255 0,00318 0,00239 0,051 0,0191 0,0143 0,00955

f, Гц

Контрольные вопросы:

1. Какими параметрами характеризуется синусоидальные ток и напряжение?

2. Что такое векторная диаграмма?

3. Как определить комплексное сопротивление ветви?

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Date: 2015-12-11; view: 1749; Нарушение авторских прав
Понравилась страница? Лайкни для друзей:

mydocx.ru - 2015-2024 year. (0.015 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию