Параболоиды

Эллиптическим параболоидом называется поверхность, определяемая уравнением

, (24)

при условии, что р и q имеют одинаковые знаки. В дальнейшем, для определенности, будем считать, что р>0, q>0.

При пересечении эллиптического параболоида координатными плоскостями Oxz и Oyz получатся, соответственно, параболы

и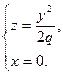

а при пересечении плоскостью z = h (h >0) - эллипс

с полуосями и (рис. 11). В случае

p = q получим параболоид вращения

. (25)

Поскольку х и у входят в уравнение (24) в четных степенях, эллиптический параболоид имеет две плоскости симметрии: Oxz и Oyz.

Рис.11

Рис.12.

Гиперболическим параболоидом называется поверхность, определяемая уравнением

. (26)

при условии, что р и q имеют одинаковые знаки. (В дальнейшем, для определенности, будем считать, что р>0, q>0.)

Пересекая эту поверхность плоскостью Oxz, получим параболу

(27)

(рис.12.)

При пересечении гиперболического параболоида плоскостью x = h получится парабола

или

При различных значениях h получится целое семейство парабол, лежащих в плоскостях, параллельных плоскости Oyz и имеющих одинаковый параметр q.

Гиперболический параболоид можно рассматривать как поверхность, описываемую движением любой из этих парабол при условии, что плоскость движущейся параболы остается параллельной плоскости Oyz, ось симметрии параболы остается в плоскости Oxz, а вершина движется по параболе (27). Пересекая гиперболический параболоид плоскостью z = h, получим (при ) гиперболу:

или

На рис. 12 показано расположение этой гиперболы для двух случаев: h >0 и h <0. При h = 0, т. е. при пересечении гиперболического параболоида координатной плоскостью Оху, получится линия, уравнение которой в плоскости Оху имеет вид:

.

Последнее уравнение равносильно системе двух уравнений

, .

Это означает, что гиперболический параболоид пересекается с плоскостью Оху по двум прямым:

и

лежащим в плоскости Оху и проходящим через начало координат. Кроме этих двух прямых, существуют и другие прямые, полностью лежащие на гиперболическом параболоиде. Более того, как и в случае однополостного гиперболоида, можно показать, что через каждую точку гиперболического параболоида проходит по одной прямой каждого из двух семейств прямых:

и

где k и l - произвольные параметры.

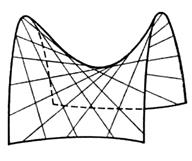
Таким образом, гиперболический параболоид можно рассматривать как поверхность, составленную из прямых линий (Рис. 13).

Замечание. Поверхности, составленные из прямых линий, называются линейчатыми. Таким образом, цилиндрические и конические поверхности, а также однополостный гиперболоид и гиперболический параболоид являются линейчатыми поверхностями.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Беклемешев Д.В. Курс аналитической геометрии и линейной алгебры - М. Наука, 1980.

2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической Геометрии - М. Наука, 1980.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая мате- матика в упражнениях и задачах, 1 ч. - М. Высш. шк., 1986.

4. Изосов А.В., Изосова Л.А. Векторная алгебра и аналити- ческая геометрия - Учебное пособие, Магнитогорск, 2001.

5. Щипачёв В.С. Высшая математика - М., Высш. шк., 1985.

6. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики - М., Высш. шк., 1978.

СОДЕРЖАНИЕ

ГЛАВА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ…………… 3

§ 1. Матрицы и алгебраические действия с ними. ………… 3

§ 2. Определители матриц и их свойства. …………………….. 8

§ 3. Обратная матрица. …………………………………………….. 16

§ 4. Системы линейных алгебраических уравнений. ………… 21

ГЛАВА 2. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. ………….. 46

§ 1. Вектор. Алгебраические действия с векторами. ………. 46

§ 2. Системы координат на прямой, в плоскости и в

пространстве …………………………………………………… 49

§ 3. Нелинейные операции над векторами. ………………….. 57

§ 4. Понятие евклидова пространства. ………………………… 69

ГЛАВА 3. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ. 72

§ 1. Прямая линия на плоскости. …………………………………72

§ 2. Взаимное расположение прямых на плоскости. ……….. 75

§ 3. Плоскость в пространстве. …………………………………... 79

§ 4. Прямая в пространстве. ……………………………………… 83

§ 5. Взаимное расположение прямой и плоскости в

постранстве. ……………………………………………………… 87

§ 6. Линии второго порядка на плоскости. …………………….. 97

§ 7. Полярная система координат. …………………………….... 114

§ 8. Поверхности второго порядка. ……………………………. 122

БИБЛИОГРАФИЧЕСКИЙ СПИСОК …………………………… 141