
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические рекомендации. Вектором (геометрическим) называется направленный отрезок
|
|
Вектором (геометрическим) называется направленный отрезок. Обозначается  ,
,  ,
, 
Отложим вектор так, чтобы его начало совпало с началом координат. Тогда координаты его конца называются координатами вектора. Обозначим  векторы с координатами (1, 0, 0), (0, 1, 0), (0, 0, 1) соответственно. Их длины равны единице, а направления совпадают с направлениями соответствующих осей координат. Будем изображать эти векторы, отложенными от начала координат и называть их координатными векторами.
векторы с координатами (1, 0, 0), (0, 1, 0), (0, 0, 1) соответственно. Их длины равны единице, а направления совпадают с направлениями соответствующих осей координат. Будем изображать эти векторы, отложенными от начала координат и называть их координатными векторами.

Теорема. Вектор  имеет координаты (x, y, z) тогда и только тогда, когда он представим в виде
имеет координаты (x, y, z) тогда и только тогда, когда он представим в виде  /
/
| Действия над векторами | Запись | Пример |
1. Результатом умножения вектора  на число на число  является вектор является вектор 
|  , ,  – число, то – число, то 
|  ; ; 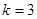 , тогда , тогда


|
| 2. Сложение векторов. Вычитание векторов. |  ; ; 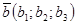


|  ; ;  , тогда , тогда
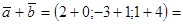

|
| 3. Нахождение координат вектора. При определении координат вектора из соответствующих координат его конца вычитают координаты начала |  ; ; 

|  , , 
 ; ;

|
| 4. Длина вектора. | 

| 

|
| 5. Условие коллинеарности векторов: векторы коллинеарны, если их соответствующие координаты пропорциональны. |  и и 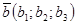

|  , , 

 векторы коллинеарны векторы коллинеарны
|
| 6. Скалярное произведение векторов – это число равное произведению длин векторов на косинус угла между ними. Скалярное произведение векторов равно сумме произведений одноименных координат. |

 и и 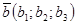

|
 ; ; 
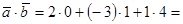

|
| 7. Косинус угла между векторами. |  ; ; 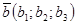

| |
| 8. Условие перпендикулярности векторов: векторы перпендикулярны, если их скалярное произведение равно нулю. |  ; ; 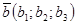


|  ; ; 


|
Date: 2015-12-10; view: 546; Нарушение авторских прав