Основное уравнение в квантовой механике

Некоторые понятия классической физики при переходе к микромиру теряет свою определенность, становясь попарно–противоречивыми, взаимоисключающие друг друга (частица – волна, координата- импульс и другие). Однако, для полноты описания ими приходится одновременно пользоваться. При этом они становятся взаимодополняющими друг друга и приобретают качественно новое содержание. Этот факт квантомеханической дополнительности накладывает определенные условия накладывает определенные условия на формулировку основных законов микромира.

В классической физике всякое описание явления одновременно пространственно-временное и динамически причинное. Например, в механике Ньютона описание движения материальной точки пространственно-временное, т.к. в любой момент времени t заданы

в пространстве ее радиус-вектор 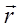(координаты) и . В тоже время описание является динамически причинным и подчиняется следующей схеме:

	Причина Начальные:   to, , o		Закон причинности Уравнение движения: = (, , t)		Следствие Конечное состояние: t, , ,

При этом абсолютизируется как понятие пространства и времени, так и понятие причинности, а существование объектной случайности отрицается.

Во всеобщей связи предметов и явлений материального мира можно выделить главные - определяющие связи–причины и второстепенные, которыми, как правило, пренебрегают. Поведение объектов и течение явлений, в основном, определяется причинами. При таком подходе все материальные события (материальная действительность) распадается на множество не связанных между собой причинно-следственных рядов. Ряды в случае пересечения приводят к появлению объективно–случайного явления (с “точки зрения” каждого из рядов). Для объяснения подобных явлений необходимо учитывать не только внутренние динамические причины, но и внешние объективно-случайные факторы (второстепенные связи).

Строгое динамическое причинное описание любой конечной системы возможно лишь при условии ее абсолютной изолированности, исключающей действие объективно-случайных факторов. При этом должно быть исключено всякое наблюдение этой системы, т.к. взаимодействие с измерительным прибором будет нарушать ее изолированность.

Основой пространственно-временного описания поведение системы является ее наблюдение в пространстве и времени, невозможное при изолированности системы. Отсюда следует взаимоисключаемость пространственно-временного динамически причинного описания. В классической физике этот вывод игнорировался, в квантовой физике этого сделать нельзя, т. к. нельзя ни пренебречь, ни учесть взаимодействие микрообъекта со средствами наблюдения.

Рассмотренная ситуация была выражена в 1928 г. Н. Бором в виде так называемого принципа дополнительности: существует два типа экспериментальных установок, измеряющих либо импульсно-энергетические (динамически причинные), либо пространственно-временные соотношения. Одновременное использование их невозможно.

Вместо классического динамически причинного описания состояний микрообъектов вводится новая характеристика их состояний - волновая функция Y(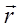, t), имеющая вероятность, статический смысл. Отсюда следует, что при переходе от классической механики к квантовой на смену динамической причинности приходит статическая.

Это, означает например, что у изолирующего микрообъекта значение волновой функции в последовательные моменты времени должно образовывать причинно-следственный ряд и из значения функции Y(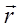, t) однозначно вытекает ее значение Y(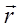, t+dt), на основе некоторого закона причинности, называемого основным уравнением квантовой механики.

Найдем общий вид этого уравнения для случая справедливости следующего разложения волновой функции в ряд Макларена:

(1)

Очевидно, для Y(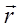, t+dt), необходимо, чтобы известному значению Y(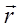, t)/¶t, также определить через Y(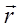, t), т. е., чтобы существовало дополнительное уравнение

(2)

где 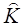- подлежащий определению оператор.

Если он будет найден, то уравнение (2) будет определять временной ход изменения состояния микрообъекта в определенных внешних условиях. Последовательная смена состояния этого микрообъекта будет образовывать причинно-следственный ряд во времени. Потому уравнение (2) будет представлять собой закон статической причинности и становится основным уравнением квантовой механики. Схема статистики причинного описания может быть представлена в виде:

`

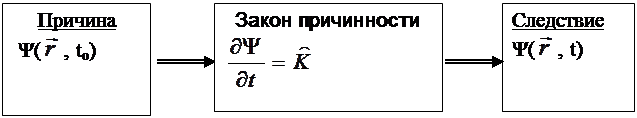
Волновое соотношение неопределенностей и его связь с

соотношение неопределенностей Гейзенберга.

Запишем уравнение плоской бегущей плоской волны распространяющейся вдоль оси x

y(x,t) = y_ocos(ωt- 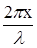)= y_ocos(γt-æx) (1)

Если это уравнение относится к волне де-Бройля, имеющей импульс p= hæ(æ= 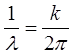) и энергию E = hλ, то его можно представить в виде:

y(x,t)= y_ocos (Et-px) (2)

Представим его в комплексной форме:

Y(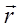, t)= Y_oe 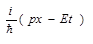(3)

Физический смысл при этом имеет действительная часть этого выражения ReY(x, t)= y(x, t) и величина YY^*=÷Y_о÷².

Эквивалентность выражение (3) и (4) показывает, что они описывают как движение частицы, что соответствует корпускулярно-волновому дуализму материи. Однако такое описание обладает существенным недостатком оно –фиксирует определенный импульс Р и энергию Е частицы, но не определяет ее локализацию в пространстве, т. к. x и t при этом неопределенны.

Для описания локализации частицы в некоторой области пространстве x₁, x₂ в некотором промежуточном времени Dt=t₂-t₁ необходимо ограничить волну де-Броля этими пределами. Волновой процесс, локализованный в некоторой области пространства в некоторый момент времени называется волновым пакетом. Он может быть представлен математически в виде суперпозиции большого числа монохроматических волн:

Y(x, t)=ò Y_o(æ)e^2pi(æx-γt) dæ (4)

Если предположить, что амплитуда Y_o(æ) является медленно меняющейся функции æ, отличной от нуля лишь в интервале æ_о, æ_о+Dæ, то можно принять:

æ_о+Dæ æ_о+Dæ

Y(x, t)= ò Y_o(æ)exp(2pi(æx-gt)dæ ≈ 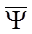_o ò(æ) exp(2pi(æx-gt)dæ

æ_о æ_о

Разложим частоту g_æ=g(æ) в ряд Тейлора по степеням ξ= æ- æ_o

g(æ)≈ g(æ_o) +(dg/dæ)_æo(æ- æ_o)+…= g_o+(dg/dæ)_oξ (6)

Преобразуем подынтегральное выражение (5) к новой переменной ξ:

exp(2πi(æx-g_æt)≈ exp(2πi(æ_ox-g_ot) exp(2πi(x-(dg/dæ)_ot)ξ

Тогда: Δk

Y(x, t)≈ 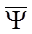_o(æ)ò exp(2πi[x-(dg/dæ)]_o ξ)dξ exp(2πg(æ_ox-g_ot)

Первые два сомножителя (подчеркнуты) можно рассматривать как комплексную амплитуду волны материи:

Δæ

Y(æ, x, t)= 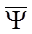_o(æ) ò exp(2πi[x-(dg/dæ)_o ]ξ) dξ (7)

Ее действительная часть

Δæ

ReY(æ, x, t)= Y_R=Re 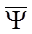_o(æ) ò exp(2πi[x-(dg/dæ)_o ]ξ) d =

= Y_OR ò cos[2π(x-(dg/dæ)_o t) ξ] dξ =

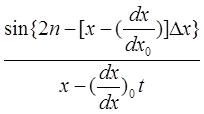
Представлена на рисунке 10.2б.-1 для t = t₀

y

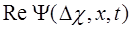
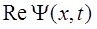
х

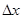
Рис.10.2б-1

Координата x₀ центра пакета в момент времени t₀ определяется равенством:

x-(dg/dæ)_o t₀ = 0 ═> x = (dg/dæ)_o t₀ (9)

С течением времени t₀ будет расти и пропорционально будет расти x₀-пакет пакет будет перемещаться с групповой скоростью:

U = dx_o/ dt_o= (dg/dæ)_o (10)

Групповая скорость не равна фазовой

V = λγ = γ/æ (11)

Из (11) следует

λ= v æ

Групповая скорость и не равна фазовой.

(11)

Из (11) следует 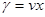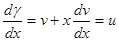(12)

Второе слагаемое в (12) является мерой дисперсии волн. Поскольку фотоны в вакууме движутся с одинаковой скоростью (дисперсия отсутствует), то для них

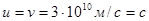(13)

Для вещественной среды с показателем преломления 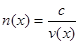получаем

и (14)

При нормальной дисперсии 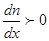и скорость фотона (15)

Для частиц вещества энергия (16),

Где V –потенциальная энергия.

Частота длины волны Де-Бройля (волны материи):

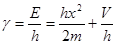(17)

Отсюда следует, что групповая скорость волн материи

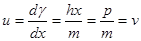(18)

т.е. равна скорости самой частицы!

Э. Шредингер предложил считать, что всякая частица есть ничто иное, как волновой пакет волн материи.

Определим размер пакета 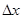в момент времени 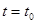. Очевидно, он равен расстоянию между двумя ближайшими к центру 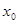точками и , в которых 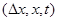равна 0. Для этих точек 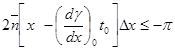и

Разность этих выражений даёт 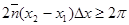, откуда (19)

Т.о. размеры пакеты обратно-пропорциональны величине интервала 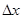волновых чисел 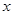. Определим длительность пакета , т.е. промежуток времени, в течение которого пакет проходит через фиксированную точку пространства, например, (20)

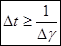Учитывая (16), получим , т.е. (20)

Следовательно, длительность волнового пакета обратно пропорциональна величине интервала частот слагаемых волн.

Следует учесть, что размер 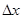и длительность волнового пакета не являются постоянными, а возрастают пакет расползается с течением времени, что можно доказать строго, если учесть слагаемые, отраженные в разложении в ряд Тейлора.

Перепишем соотношения (19) и (20) иначе

(21)

(22)

Соотношения (21), (22) называются волновыми соотношениями неопределённости.

Их физический смысл: чем ближе группа слагаемых волн по своему составу к монохроматической волне , тем сильнее расплывается пакет

, а это значит, что теряет смысл её пространственная локализация. И наоборот – чем более неоднородной становится группа волн по спектральному составу , тем более точно она может быть локализована в пространстве и времени .Т.о. из анализа соотношений (21), (22) вытекает следующий вывод: всякий реальный волновой процесс конечен в пространстве и времени, т.е. не может быть монохроматическим.

Поскольку волновое движение ограничено соотношениями (21), (22), то они будут сказываться и на поведении микрочастиц. Умножая обе части этих выражений на постоянную Планка , получим соотношения неопределённостей Гейзенберга:

(23),(24)

Из (23) и (24) следует, что принципиально невозможно одновременно точно измерить у микрообъекта координату и импульс или же произвести мгновенное

Точное измерение энергии.

Предельно точной локализации микрообъекта 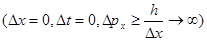более всего соответствует корпускулярное представление о нём.

Точному измерению импульса объекта 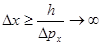соответствует волновое представление о нём.

Рассмотрим два примера, иллюстрирующих по сути квазиклассический способ описания объекта на основании соотношения (23).

Пусть пуля имеет массу

Её мгновенное положение в полёте не имеет смысла определить точнее, чем с неопределённостью Тогда неопределённость в определении скорости 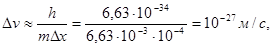что лежит далеко за пределами возможностей современной измерительной техники. При увеличении 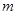, будет уменьшаться. Следовательно: соотношение неопределённостей не играет никакой роли при описании движения микрообъектов.

Если предоставить такой микрообъект как электрон в виде частицы, то неопределённость в определении его положения не должна быть по порядку величины больше его диаметра Поэтому неопределённость в определении его скорости.

Физический смысл соотношения (24) заключается в том, что невозможно мгновение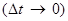

Измерение энергии микрообъекта, т.к. 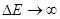. Наоборот, для точного измерения энергии необходимо бесконечно медленно производить измерение .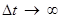

Вывод: соотношения неопределённостей В. Гейзенберга являются отражением объективной деятельности копускулярно-волнового дуализма материи, подтверждённого экспериментально. Их следует принять как постулат и положить в основу новой неклассической квантовой механики.

Теория относительности ещё более ограничивает применение классических понятий в микромире и приводит к выводу, что само понятие длины имеет смысл с точностью до (так называемый “классический радиус электрона”), а понятие промежутка времени с точностью до .

Date: 2015-11-15; view: 364; Нарушение авторских прав