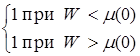Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Принцип Паули д: в данной системе тождественных фермионов любые два не могут одновременно находиться в одном и том же состоянии (т.е. в одной и той же ячейке фазового объёма)
|
|
Фермионы (электрон, мюон, кварки, протон, нейтрон, нейтрино и т.д.) подчиняются статистике Ферми-Дирака; бозоны (фотоны, гравитоны, бозонные резонансы, составные частицы из чётного числа фермионов и т.д.) – Бозе-Эйнштейна. Бозе Шатындрант (1894-1974) – индийский физик; 1924-1925 работал в Париже у М. Склодовской-Кюри; один из создателей статистики бозонов. Вывел закон Планка для теплового излучения.
Различия между статистиками Максвелла-Больцмана, Ферми-Дирака, Бозе-Эйнштейна понятны на примере подсчёта числа возможных состояний двух частиц (рис. 13.4).
| Классическая статистика Максвелла-Больцмана (различимые частицы) | Квантовая статистика Ферми-Дирака (неразличимые частицы, подчиняющиеся принципу Паули) | Квантовая статистика Бозе-Эйнштейна (неразличимые частицы) | |||||||||
| Ab | – | a | a | aa | – | ||||||
| – | ab | – | aa | ||||||||
| A | b | a | a | ||||||||
| B | a | ||||||||||
| 4 состояния | 1 состояние | 3 состояния | |||||||||
Рис.13.4
Схема вывода функций распределения Ферми-Дирака и Бозе-Эйнштейна следующая:
- методами комбинаторики находят термодинамическую вероятность состояния W b – число способов, которыми N i неразличимых объектов можно разместить по Z i ячейкам (состояниям с энергиями W i);
- поскольку равновесное состояние является наиболее вероятным, методом неопределённых множителей Лагранжа находят экстремум функции ln W b;
- после потенцирования полученных выражений приходят к искомым соотношениям.
Прежде чем записывать квантовые функции распределения, обобщим I начало термодинамики. Изменение внутренней энергии системы d U может происходить не только за счёт сообщения ей тепла d Q = T d S и совершения работы над системой d A=- p d V, но и в процессе массообмена с внешней средой:
d U = T d S - p d V + m d N. (13.13)
Величина m =  (13.14) называется химическим потенциалом и представляет собой изменение внутренней энергии системы, приходящееся на одну частицу, при изохорно-изоэнтропийном процессе.
(13.14) называется химическим потенциалом и представляет собой изменение внутренней энергии системы, приходящееся на одну частицу, при изохорно-изоэнтропийном процессе.
Можно показать, что функции распределения Бозе-Эйнштейна и Ферми-Дирака имеют соответственно следующий вид:
fM-Б (W) > 0,
 , (13.15)
, (13.15)
 . (13.16)
. (13.16)
Для бозонов f Б-Э(W) > 0, для фермионов 0 £ f Ф-Д(W) £ 1. Функции распределения в классической и квантовой статистике, введенные как среднее число частиц в данном энергетическом состоянии, могут быть выражены единой формулой:
 (13.17)
(13.17)
Если W >> m и  >> d, то квантовые статистики переходят в классическую, которую можно рассматривать как их предельный случай.
>> d, то квантовые статистики переходят в классическую, которую можно рассматривать как их предельный случай.
Газ называется вырожденным, если его свойства отличаются от свойств классического идеального газа. В вырожденном газе происходит взаимное квантово-механическое влияние частиц, обусловленное их неразличимостью. Степень вырождения характеризуют параметром вырождения A=  , тогда:
, тогда:
 . (13.18)
. (13.18)
Если А << 1, то  / А <<1 и функция fkв с точностью до множителя превращается в функцию распределения Максвелла fM-Б: fkв (W) @ А fМ-Б (W).
/ А <<1 и функция fkв с точностью до множителя превращается в функцию распределения Максвелла fM-Б: fkв (W) @ А fМ-Б (W).
Сравнительно легко оценить температурный критерий вырождения газа. Вырождение обычных газов сказывается при низких температурах, что несправедливо для электронного и фотонного газа.
Параметр вырождения находится из условия нормировки функции распределения
 , (13. 19) означающего сохранение в системе общего числа частиц:
, (13. 19) означающего сохранение в системе общего числа частиц:
 .
.  (13.20)
(13.20)
Условие малости вырождения: А <<1.
|
Температурой вырождения ТВ называется температура, при которой вырождение становится существенным. Она определяется из условия А =1, откуда
 . (13.21)
. (13.21)
Т.o. температурный критерий вырождения имеет вид:
Т £ ТВ - система частиц вырождена и подчиняется
квантовым статистикам;
Т>>ТВ - система не вырождена и подчиняется
классической статистике. 
Примеры:
а) фотонный газ, m = O, TВ ® ¥. Фотонный газ при любых конечных температурах является вырожденным.
б) электронный газ в металлах no @1029 м-3, ТВ @2×104 К, m =9,1×10-31кг. Только при Т ® Тв (т.е. выше десятков тысяч градусов Кельвина) электроны металла подчинялись бы классической статистике Максвелла-Больцмана. Но при таких температурах металл не может существовать в конденсированном состоянии. Классическое описание приводит в ряде случаев к противоречию с опытными данными.
в) электронный газ в полупроводниках, no @ 1018м-3, ТВ @ 10-4К - электронный газ в полупроводниках является невырожденным и подчиняется классической статистике.
г) атомные и молекулярные газы. Для водорода  при нормальных условиях (Т @ 300К ,no @ 3 1025м-3) ТB @ 1К; для более тяжелых газов ТB < 1К. Газы при нормальных условиях не бывают вырожденными. Вырождение газов, связанное с их квантовыми свойствами, проявляется в меньшей степени, чем отклонение от идеальности, вызванное межмолекулярным взаимодействием.
при нормальных условиях (Т @ 300К ,no @ 3 1025м-3) ТB @ 1К; для более тяжелых газов ТB < 1К. Газы при нормальных условиях не бывают вырожденными. Вырождение газов, связанное с их квантовыми свойствами, проявляется в меньшей степени, чем отклонение от идеальности, вызванное межмолекулярным взаимодействием.
Отличие свойств вырожденного электронного газа от обычного понятна на следующем примере. Невырожденный тем идеальнее, чем меньше потенциальная энергия взаимодействия его молекул по сравнению с кинетической, что наблюдается при малых плотностях газа. Потенциальная энергия взаимодействия электронов U =  , где a - среднее расстояние между электронами a ~
, где a - среднее расстояние между электронами a ~  . Следовательно, U~
. Следовательно, U~ 
 . Кинетическая энергия электронов Ek~
. Кинетическая энергия электронов Ek~  . Следовательно с ростом концентрации электронов Еk растет быстрее, чем U. Поэтому электронный газ ближе к идеальному при больших концентрациях.
. Следовательно с ростом концентрации электронов Еk растет быстрее, чем U. Поэтому электронный газ ближе к идеальному при больших концентрациях.
§ 13.3. Примеры использования квантовых статистик.
1. В полости объема V при Т=const в состоянии термодинамического равновесия со стенками находится излучение абсолютно-чёрного тела. Поскольку для фотонов спин равен  , его можно рассматривать как фотонный газ, подчиняющийся статистике Бозе-Эйнштейна. Для фотонов m = О и распределение Бозе-Эйнштейна имеет вид:
, его можно рассматривать как фотонный газ, подчиняющийся статистике Бозе-Эйнштейна. Для фотонов m = О и распределение Бозе-Эйнштейна имеет вид:
¦Б-Э=  . (13.22)
. (13.22)
Это объясняется непостоянством числа фотонов в полости и их зависимостью от температуры. Равновесность излучения достигается за счет излучения и поглощения стенками полости.
Запишем функцию распределения Планка для излучения абсолютно черного тела:
 П (l,T) =
П (l,T) = 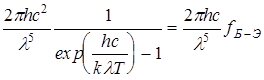 . (13.23)
. (13.23)
Следовательно, распределение Планка вытекает из распределения Бозе-Эйнштейна.
Запишем функцию распределения Вина:
 В (l,T)=
В (l,T)=  . (13.24)
. (13.24)
Cледовательно функция Вина вытекает из распределения Максвелла-Больцмана.
 2. Анализ распределения Ф-Д для электронного газа при Т =0 К. Пусть при Т =0 К m=mо. Если Т ® 0, W < m o, то ¦Ф-Д =1; если Т ® 0, W > mo, то ¦Ф-Д =0. Смысл этого результата: при Т =0 К все энергетические состояния равномерно заполнены по одному электрону в каждом состоянии вплоть до энергии WF =mo, которая называется энергией Ферми и представляет собой максимальную энергию, которую могут иметь электроны в металле при Т =0 К (рис. 13.6).
2. Анализ распределения Ф-Д для электронного газа при Т =0 К. Пусть при Т =0 К m=mо. Если Т ® 0, W < m o, то ¦Ф-Д =1; если Т ® 0, W > mo, то ¦Ф-Д =0. Смысл этого результата: при Т =0 К все энергетические состояния равномерно заполнены по одному электрону в каждом состоянии вплоть до энергии WF =mo, которая называется энергией Ферми и представляет собой максимальную энергию, которую могут иметь электроны в металле при Т =0 К (рис. 13.6).
|
(13.25)
Распределение Ферми-Дирака нечувствительно к изменению температуры. Функция ¦Ф-Д (W) искажается в интервале 2 kT, так что ¦Ф-Д (m)=1/2 (рис.13.7).
|
Зависимость химического потенциала m от температуры имеет вид:
 (13.26)
(13.26)
WF>>kT, поэтому m (T) @ WF, A @ exp 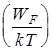 >>1 - электронный газ в металле всегда вырожден.
>>1 - электронный газ в металле всегда вырожден.
С помощью распределения Ферми-Дирака можно объяснить вопросы, связанные с распределением импульсов, скоростей, энергии электронов, теплоёмкости электронного газа, сверхпроводимости металлов.
Внутренняя энергия моля электронного газа:
 . (13.27)
. (13.27)
Чтобы оценить результаты, даваемые квантовой статистикой, сравним их с классической электронной теорией. Её основными законами являются законы Ома и Джоуля-Ленца в дифференциальной форме:
 , (13.28)
, (13.28)
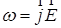 , (13.29) где удельное сопротивление:
, (13.29) где удельное сопротивление:
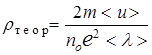 . (13.30) Здесь < l > - средняя длина свободного пробега электронов,
. (13.30) Здесь < l > - средняя длина свободного пробега электронов,
< u > - средняя арифметическая скорость теплового движения.
Основными недостатками электронной теории являются невозможность объяснить:
- экспериментально наблюдаемую в широком интервале температур линейную зависимость между удельным сопротивлением r и абсолютной температурой
r экс ~ T. (13.31)
Поскольку < u > ~ T 1/2, то
r экс ~ T 1/2. (13.32)
- значение молярной теплоёмкости металлов.
Согласно экспериментальному закону Дюлонга и Пти:
С М мет.Экс. @ С М тв.м. @  @
@  . (13.33)
. (13.33)
В соответствии с классической теорией:
С М мет.теор. @  = С М ион.кр.реш. + С м Эл.газа = =
= С М ион.кр.реш. + С м Эл.газа = =  +
+  @
@  +
+  =
=  , (13.34) т.е. электронная составляющая теплоёмкости металлов как бы отсутствует.
, (13.34) т.е. электронная составляющая теплоёмкости металлов как бы отсутствует.
В соответствии с квантовой теорией электропроводности металлов удельная электропроводность определяется соотношением:
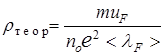 , (13.35)
, (13.35)
где < l F> - средняя длина свободного пробега электрона, имеющего энергию Ферми;
uF - скорость теплового движения такого электрона.
 , (13.36) где Е - модуль упругости Юнга;
, (13.36) где Е - модуль упругости Юнга;
d - период кристаллической решётки.
Подставляя (13.36) в (13.31), получим:
r теор.=  Т ~ Т. (13.37)
Т ~ Т. (13.37)
Для Ag r теор ~5·107 Ом-1м-1, r экс ~6·107 Ом-1м-1. При очень низких температурах формула (13.37) не справедлива. В этом случае < l F>~1/ T 5 и r теор ~ Т 5.
Молярная теплоёмкость электронного газа
С М Эг.кв. =  =
=  . (13.38)
. (13.38)
Классическая физика даёт результат:
С М Эг.кв. =  . (13.39)
. (13.39)
Отсюда
 . (13.40)
. (13.40)
Для комнатных температур kT/W F ~ 0,01, поэтому
 ~0,03, (13.41) т.е. теплоёмкость электронного газа ничтожно мала. Это связано с тем, что в процессе изменения внутренней энергии электронного газа при нагревании участвует незначительное число электронов, находящихся в области спада функции распределения f Ф-Д.
~0,03, (13.41) т.е. теплоёмкость электронного газа ничтожно мала. Это связано с тем, что в процессе изменения внутренней энергии электронного газа при нагревании участвует незначительное число электронов, находящихся в области спада функции распределения f Ф-Д.
Приложения. Дополнительные разделы квантовой механики.
Date: 2015-11-15; view: 431; Нарушение авторских прав