
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Практична робота № 11
|
|
Тема: Розв’язання лінійних однорідних диференціальних рівнянь 2-го порядку зі сталими коефіцієнтами.
Мета: Навчитись розв’язувати лінійні однорідні диференціальні рівняння 2-го порядку зі сталими коефіцієнтами.
Теоретичні відомості:
Рівняння виду у′′+ ру′+qy=0 (1)називається лінійним однорідним диференціальним рівнянням 2-го порядку з сталими коефіцієнтами
Розв’язки будемо шукати у вигляді:
y=ekx; k – стала.
y’=kekx; y”=k2ekx;
ekx (k2+pk+q)=0; /:ekx≠0;
k2+pk+q=0; - характеристичне рівняння.
Позначимо корені через k1,k2.
Оскільки характеристичне рівняння квадратне, то в залежності від знака дискримінанта можливі три варіанта:
31. D>0, то корені рівняння дійсні і різні
y1=еk1x; y2=еk2x;
y=C1 еk1x+C2 еk2x, C1,C2 – сталі.
2. D<0 то корені рівняння комплексні:
k= 
y1= 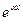 sin
sin  x; y2=
x; y2= 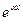 cos
cos  x;
x;
y=edx(C1sin  x+C2 cos
x+C2 cos  x).
x).
3. У випадку нульового дискримінанта корені рівняння дійсні і рівні:
y1=ek1x; y2=xek1x,
y=ek1x(C1+xC2).
Загальний розв’язок: Y=y1c1 + y2c2
• Приклад.
Розв'язати рівняння у" +4у' + Зу = 0.
Розв'язання.
Складемо характеристичне рівняння к2 + 4к + 3 = 0.,
розв'язуючи його за теоремою Вієта, знайдемо корені к1 = -3, к2 =-1. Оскільки отримані корені різні, то у1= е-3х, у2 = е-х. Функції у1 ї у2 є лінійно незалежними. Отже, загальний розв'язок вихідного рівняння набуває вигляду
v = С1 ек1 Х + С2 ек2 Х, або у = С1 е-3х+ С2 е-х
Відповідь: у = С1 е-3х+ С2 е-х
Завдання до виконання:
1.Знайти загальні розв’язки рівняння
1. у′′+ 3у′-4y=0
2. у′′-9у′+14y=0
3. у′′+ 6у′+8y=0
4. у′′-16y=0
5. у′′-y=0
6. у′′+ 8у′+16y=0
7. у′′-у′+⅓y=0
8. у′′-6у′+45y=0
9. у′′+ 4у′+8y=0
10. у′′-5у′+6y=0
11. у′′-6у′+45y=0
2. Знайти частинні розв’язки рівняння
1. у′′-9у′=0, якщо y=2 і у′=6 при x=0
2. у′′-у′-2y=0, якщо y=3 і у′=0 при x=0
3. у′′+6у′+5y=0, якщо y=1 і у′=1 при x=0
4. у′′-10у′+25y=0, якщо y=2 і у′=8 при x=0
5. у′′+3у′+2y=0, якщо y= -1 і у′=3 при x=0
6. у′′-6у′+9y=0, якщо y=2 і у′=1 при x=0
Контрольні запитання:
1. Що називається лінійним однорідним диференціальним рівнянням 2-го порядку з сталими коефіцієнтами?
2. Як складається характеристичне рівняння?
3. В якому вигляді шукають розв’язки, якщо дискримінант додатній?
4. В якому вигляді шукають розв’язки, якщо дискримінант від’ємний?
5. В якому вигляді шукають розв’язки, якщо дискримінант дорівнює 0?
6. Як записати загальний розв’язок рівняння?
Date: 2015-10-19; view: 385; Нарушение авторских прав