Перспектива плоских фигур и геометрических тел

Задача 13. Построение перспективы окружности.

Построить на картине перспективу окружности, лежащей в совмещенной предметной плоскости Н", диаметр которой равен 50мм. Границы совмещенной предметной плоскости можно не изображать, но каждую фигуру, расположенную ниже основания картины ОО1, будем считать лежащей в совмещенной предметной плоскости Н".

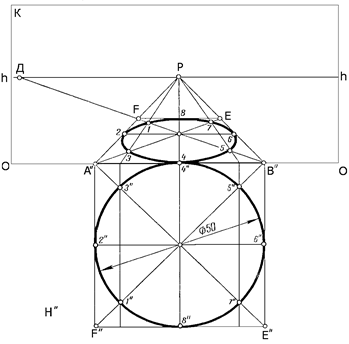
		Начертим касательные к заданной окружности так, чтобы она вписалась в квадрат А"В"Е"F"
	В квадрате проведем диагонали А"Е" и В"F" и построим на картине перспективу квадрата.
	На пересечении диагоналей квадрата получим в перспективе его середину, через которую проведем две прямые: одну в точку Р, другую параллельно картине.
	Перспективу окружности построим по восьми точкам 1,2,3,4…, четыре из которых 2,4,6,8 будут расположены на середине сторон квадрата, а остальные на диагоналях
	Через точки 1",3" и 5",7" проведем прямые до пересечения с основанием картины
	Затем построим перспективу этих прямых, на которых найдем перспективу точек 1,3 и 5,7
	Соединим плавной кривой все восемь точек
	Перспектива окружности получится в виде эллипса, вписанного в перспективу квадрата А"В"Е F.

Задача 14. Построение перспективы окружности упрощенным способом.

Упрощение состоит в том, что определяют промежуточные точки для окружности без построения самой окружности и квадрата в совмещенной плоскости Н"

		На основании картины отложим сторону АВ.
	Из середины стороны АВ проведем прямую под углом 45°
	Опустим на нее перпендикуляр из точки А.
	Затем соединим стороны АВ радиусом, равным катету образовавшегося равнобедренного прямоугольного треугольника
	Начертим полуокружность до пересечения со стороной квадрата в двух точках
	Через точки пересечения полуокружности со стороной квадрата проведем параллельные прямые в точку Р
	Эти прямые пересекутся с диагоналями квадрата в четырех искомых точках 1, 3, 5, 7
	Остальное построение видно из чертежа

На рисунке показано построение перспективы окружности в различных плоскостях.   Форма окружности сохраняется только в плоскостях, расположенных фронтально к зрителю, или параллельно картине.   В горизонтальной и профильной плоскостях перспектива окружности построена вторым (упрощенным) способом.

КУБ Задача 15(а,б).

Построить перспективу куба стоящего на предметной плоскости и удаленной от основания картины на 10мм. Сторона равна 30мм и расположена параллельно К.

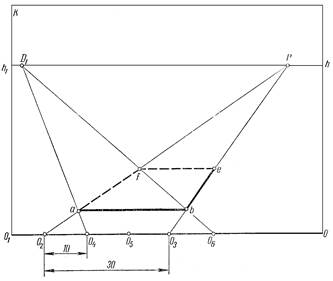
		Даны точки Р и Д1
	Построим перспективу основания куба авef. Для этого возьмем на основании картины отрезок О2О3 равный 30мм.
	Из точек О2 и О3 проведем параллельные прямые в точку Р.
	ОтрезокО2О3 разделим на три равные части точками О4 и О5
	Чтобы определить расстояние от картины до перспективы стороны АВ, надо провести прямую О4Д1, которая пересечет прямую О2Р в точке а.
	Затем от точки а отложим в глубину размер аf равный 30мм. Для этого от точки О4 отложим на основании картины отрезок О4О6 величиной 30 мм и проведем прямую из точки О6 в точкуД1.

		Перспектива точки f определяется на пересечении прямой О6Д1 с прямой О2Р
	Итак, определив перспективу двух точек а и f,проведем через них две горизонтальные прямые до пересечения с прямойО3Рв точкахв и f.
	Из полученных точек а, в, e, f восставим перпендикуляры и с помощью масштаба высоты построим перспективу вертикальных ребер куба.
	Для этого из точки О2 восставим перпендикуляр и отложим на нем отрезок О2Q величиной 30мм
	Точку Q соединим с точкой Р. Точки А и F определяются на пересечении прямой QР с вертикальными прямыми, проведенными из точек а и f.

ПАРАЛЛЕЛЕПИПЕД

Перспективу параллелепипеда, у которого одна грань параллельна картине и заданы размеры трех его сторон, строят при помощи перспективных масштабов глубины, ширины и высоты таким же образом, как и куб.

Если необходимо построить перспективу параллелепипеда по заданным размерам его сторон, когда одна грань его расположена под произвольным углом к картине, то в таком случае для определения масштаба глубины нужно использовать совмещенную точку зрения Ск и масштабные точки М и N.

Задача 16(а,б).

Построить перспективу параллелепипеда по заданным размерам его сторон ав=30мм,аg=20мм, высота Аа=10мм.

Сторона АВ расположена под произвольным углом к картине.

На картине заданы точки Р и Д1

Рис А.		Возьмем на основании картины произвольную точку О2 и проведем из нее прямую О2 F.
	На прямой О2 F в произвольном месте поставим основание а точки А
	Построим совмещенную точку Ск и начертим угол F Ск F1 равный 90°
	Из точки а проведем прямую в точку F1, угол F1 а F будет прямым.
	Чтобы построить перспективу отрезка ав, равного 30мм, определим масштабную точку М. Через точку М и а проведем прямую до пересечения с основанием картины в точке О3
	Из точки О3 на основании картины отложим отрезок О3О4, равный 30мм

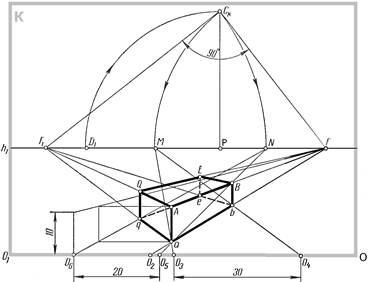
Рис Б.		Из точки О4 проведем прямую О4М, которая в пересечении с прямой О2 F определит точку в
	Из полученной точки в проведем прямую в точку схода F1
	Для построения перспективы стороны аg определим масштабную точку N. Точки N и а соединим прямой и продолжим до ее пересечения с основанием картины в точке О5.
	От точки на основании картины отложим отрезок О5О6, равный 20мм.
	Через точку О6 проведем прямую в точку N.
	Прямая ОN пересечется с прямой вF в точке g
	Точка е будет находиться на пересечении прямой gF с прямой F1 в
	Далее из каждой найденной точки восставим перпендикуляры и по масштабу высоты определим перспективу вертикальных ребер параллелепипеда.

ПРИЗМА Задача 17.

Построить перспективу правильной шестигранной призмы по заданным размерам: сторона АВ=20мм, ребро=15мм.

Основание а", в", е", f", g", l" расположено в совмещенной предметной плоскости Н" под произвольным углом к картине.

На картине заданы точки Р и Д1/2.

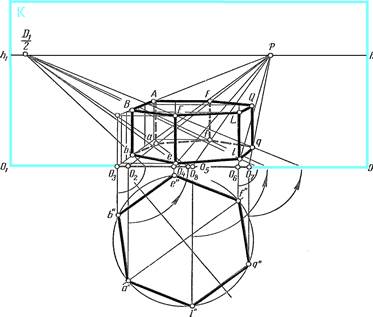
		Из каждой вершины шестиугольника а", в", е", f", g", l" проведем к основанию картины перпендикуляры, которые пересекутся с прямой ОО1 в точках О2, О3, О4, О5, О6, О7.
	Из точек О2, О3, О4, О5, О6, О7 проведем параллельные прямые в точку Р.
	Затем с помощью масштаба глубины определим перспективу каждой вершины.
	Для определения перспективы точки а, надо разделить отрезок О2 а пополам и отложить на основании картины от точки О2 его половину
	Затем из точки О8 провести прямую в точку Д1/2
	Перспектива точки а расположится на пересечении прямой О2Р с прямой, проведенной из точки О8 в точку Д1/2
	Таким образом можно построить перспективу каждой вершины шестиугольника а", в", е", f", g", l" Высоту ребер призмы определим по масштабу высоты.

ПИРАМИДА Задача 18

Построить перспективу правильной четырехугольной пирамиды SABEF, состоящей из предметной плоскости, основание которой представляет собой квадрат.

Сторона расположена параллельно картине и удалена от нее на расстояние 10мм.

Размер стороны квадрата 30мм, высота пирамиды 40мм.

На картине даны точки Р и Д1.

		На основании картины ОО1 возьмем произвольную точку О2 и проведем из нее прямую в точку Р
	От точки О2 отложим отрезок О2О3 равный 30мм
	Соединим прямой точки О3 и Р
	Затем с помощью перспективного масштаба глубины определим перспективу точки A
	Аналогично построим перспективу точки F, а затем через точки A и F проведем прямые, параллельные картине до пересечения с прямой О3Р в точках B и E.
	В полученной перспективе квадрата начертим диагонали AE и BF
	Из точки пересечения диагоналей квадрата восстановим перпендикуляр, на котором по масштабу высоты определим перспективу вершины S
	Из вершины S проведем прямые SA, SB, SE, SF, которые будут ребрами пирамиды SABEF

КОНУС Задача 19

Построить перспективу вертикально стоящего прямого кругового конуса диаметром основания 50мм.

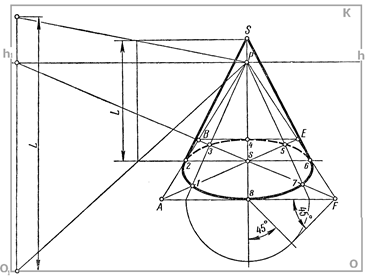
		Сначала строят перспективу квадрата ABEF со стороной, равной диаметру заданной окружности
	Затем вписывают в квадрат окружность по восьми точкам
	Из центра окружности восстанавливают перпендикуляр
	По масштабу высоты определяют перспективный размер L -высоту конуса.
	Из найденной вершины конуса L проводят две касательные к его основанию.

ЦИЛИНДР Задача 20

Построить перспективу цилиндра, стоящего на предметной плоскости. Диаметр основания равен 50мм.

		Сначала строят перспективу квадрата ABEF со стороной, равной диаметру заданной окружности
	Затем вписывают в квадрат окружность по восьми точкам 1, 2, 3, 4, 5, 6, 7, 8
	Из всех восьми точек проводят образующие цилиндра
	Перспективные размеры восьми образующих определяют по масштабам высоты через построения V
	Таким образом, перспективу верхнего основания цилиндра строят по восьми точкам без дополнительного изображения перспективы квадрата.

Date: 2015-10-19; view: 7242; Нарушение авторских прав