Интервальная оценка с помощью доверительной вероятности

Для большой выборки и нормального закона распределения общей оценочной характеристикой измерения являются дисперсия D и коэффициент вариации k_в:

(8.1)

Дисперсия характеризует однородность измерения. Чем выше D, тем больше разброс измерений. Коэффициент вариации характеризует изменчивость. Чем выше k_в, тем больше изменчивость измерений относительно средних значений, k_в оценивает также разброс при оценке нескольких выборок.

Доверительным называется интервал значений х_i, в который попадает истинное значение х_д измеряемой величины с заданной вероятностью.

Доверительной вероятностью (достоверностью) измерения называется вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал, т. е. в зону а< х_д< b. Эта величина определяется в долях единицы или в процентах. Доверительная вероятность р_д описывается выражением

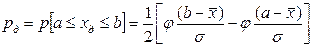
где – интегральная функция Лапласа (табл. 1.1), определяемая выражением

Аргументом этой функции является отношение m к среднеквадратичному отклонению s, т.е.

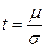(8.2)

где t – гарантийный коэффициент;

.

Если же на основе определенных данных установлена доверительная вероятность р_д (часто ее принимают равной 0,90; 0,95; 0,9973), то устанавливается точность измерений (доверительный интервал 2m) на основе соотношения . Половина доверительного интервала равна

, (8.3)

где 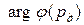– аргумент функции Лапласа, а при п< 30 – функции Стьюдента.

Доверительный интервал характеризует точность измерения данной выборки, доверительная вероятность – достоверность измерения.

Значение (1–р_д) называют уровнем значимости. Изнего следует, что при нормальном законе распределения погрешность, превышающая доверительный интервал, будет встречаться один раз из n_и измерений, где

, (8.4)

или иначе приходится браковать одно из n_и измерений.

Date: 2015-10-19; view: 1213; Нарушение авторских прав