Модели сетевой оптимизации

2.1. Метод нахождения кратчайшего пути

Рассмотрим применение сетевого подхода к решению задачи, цель которой состоит в том, чтобы найти кратчайший путь в сети. Рассмотрим алгоритм решения на примере ситуации, с которой столкнулась фирма «Инвест». Эта фирма осуществляет несколько строительных проектов в трех районах. Строительство ведется на достаточно большом (до 50 км) удалении от местоположения компании. Затраты на многочисленные ежедневные перевозки персонала, оборудования, материалов к объектам строительства и обратно существенны. Применительно к каждому объекту, альтернативы транспортных с компанией могут быть представлены сетью дорог, улиц и шоссе. Сеть (рис.2.1) отражает варианты перевозок к шести объектам строительства и от них.

Рис.2.1

Узлы сети соответствуют местоположению компании (узел 1) и объектов строительства. Дороги, улицы, шоссе представлены дугами сети. Расстояния между объектами показаны над дугами.

Фирма «Инвест» хотела бы определить пути, которые минимизировали бы общее расстояние от местоположения компании до каждого объекта, для этого необходимо определить кратчайший путь от узла 1 до каждого из всех других узлов на сети.

Метод присвоения меток. Каждому узлу присваивается метка, состоящая из двух чисел, заключенных в скобках: первое число отражает расстояние от узла 1 до данного узла, второе – номер предыдущего узла на пути от узла 1 к данному узлу. Применительно к любому помеченному узлу, можем сказать, что данный узел имеет либо постоянную, либо временную метку.

Итерации процедуры присвоения меток представлены на рис.2.2-2.9.

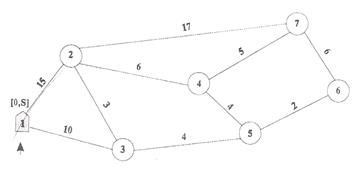
Рис.2.2

Рис.2.3

Рис.2.4

Рис.2.5

Рис.2.6

Рис.2.7

Рис.2.8

Рис.2.9

Кратчайшие пути применительно к сети компании «Инвест» представлены в таблице 2.1.

Таблица 2.1

Задача 2.1.

Вариант 1

Найдите кратчайшее расстояние от склада (7) до каждой строительной площадки.

1. Какова длина (км) кратчайшего пути от склада до строительной площадки 1?
2. Проходит ли кратчайший путь от склада к строительной площадки 1 через строительную площадку 2?

3. Какова длина (км) кратчайшего пути от склада до строительной площадки 2?

4. Проходит ли кратчайший путь от склада до строительной площадки 2 через строительную площадку 1?

Вариант 2

Ниже представлена сеть, где показатели на дугах отражают время в минутах, требующееся для проезда от одного узла до другого. Найдите пути, которые потребуют минимального времени.

1. Каково минимальное время, необходимое для того, чтобы от штаб-квартиры добраться до строительной площадки 7?

2. Проходит ли кратчайший путь от склада к строительной площадке 7 через строительную площадку 4?

3. Каково минимальное время, необходимое для того, чтобы от штаб квартиры добраться до строительной площадки 6?

Вариант 3

Найдите кратчайший путь между узлами 1 и 8 на следующей сети:

1. Какова длина кратчайшего пути?
2. Проходит ли кратчайший путь через узел 3?

Вариант 4

Нарисуйте сеть, представленную следующей таблицей.

На этой сети найдите кратчайший маршрут между узлами 1 и 10.

1. Какова длина кратчайшего пути между узлами 1 и 10?

2. Проходит ли кратчайший путь через узел 3?

Вариант 5

Компания грузовых перевозок Краснера осуществляет услуги по перевозке грузов между Воронежем (В) и райцентрами. Если компания получает заказ на обслуживание, она как можно быстрее посылает грузовик в райцентр, из которого поступил заказ. Поскольку для Каснера существенны и быстрое обслуживание, и минимальные транспортные затраты, большое значение приобретает то, что грузовик проследует из Воронежа в соответствующий райцентр по наиболее короткому маршруту. Предположим, что сеть, представленная ниже, отображает сеть дорог применительно к данной задаче. Расстояния указаны в км.

Найдите кратчайшие маршруты от Воронежа до 10 райцентров.

1. Какова длина кратчайшего пути от Воронежа до райцентра 10?

2. Какова длина кратчайшего пути от Воронежа до райцентра 8?

3. Какова длина кратчайшего пути от Воронежа до райцентра 6?

Вариант 6

Управление таксомоторных парков муниципалитета г.Москвы определило места расположения 10 основных стоянок такси на территории города. Стремясь минимизировать время на поездки, улучшить обслуживание пассажиров и рационализировать использование автомашин, руководство требует, чтобы водители использовали кратчайшие маршруты между стоянками всегда, когда это возможно. Используя сеть улиц города, представленную ниже, определите, каким маршрутом должен следовать водитель, если он отправляется от стоянки 1 на стоянку 10. Время в минутах у каждой из дуг сети.

1.Какова продолжительность в минутах кратчайшего пути от стоянки 1 до стоянки 10?

2. Проходит ли этот кратчайший путь через стоянку 10?

3. Проходит ли этот кратчайший путь через стоянку 6?

Вариант 7

Конфетная компания проводит разнообразные кондитерские продукты. Грузовики компании доставляют их по локальным заказам непосредственно в розничные торговые точки. Пока компания была небольшой, водители грузовиков свободно выбирали маршруты доставки. Однако когда бизнес приобрел солидные масштабы, затраты на транспортировку стали значительными. Пытаясь повысить эффективность операций по доставке, руководство компании хотело бы определить кратчайшие маршруты между розничными торговыми точками. Представлена сеть отражающая дороги, по которым можно следовать между точками в узлах 1 и 11.

1. Какова длина кратчайшего маршрута, которым должен следовать грузовик из узла 1 в узел 11?
2. Проходит ли кратчайший путь через узел 6?

Вариант 8

Пять узлов на сети, представленной ниже, отражают точки во времени, с первого по четвертый год. Каждый узел означает время, когда принимается решение: оставить или заменить компьютерное оборудование. Если принимается решение заменить оборудование, то одновременно должно быть принято решение, как долго это оборудование предполагается использовать. Дуга от узла 0 до узла 1 означает решение сохранить имеющееся оборудование до конца первого года, а в конце года заменить его. Дуга от узла 0 до узла 2 означает решение сохранять имеющееся оборудование в течение двух лет и заменить его в конце второго года. Числа над дугами показывают суммарные затраты, связанные с решением о замене оборудования. Эти затраты включают в себя дисконтированную цену на оборудование, текущие затраты, затраты на ремонт и т.д. Определите политику замены оборудования с минимальными затратами на четырехлетний период.

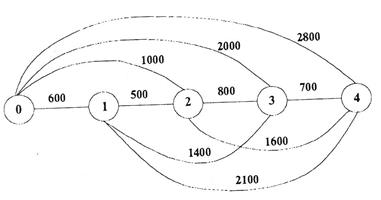
1. Каковы минимальные затраты на замену оборудования?

2. Следует ли проводить замену оборудования в году 1?

2.2.Построение коммуникационной сети

минимальной длины

Коммуникационная сеть минимальной длины, или дерево кратчайших расстояний, - это совокупность дуг сети, имеющая минимальную суммарную длину и обеспечивающая достижение всех узлов сети.

Пример

Региональный вычислительный центр должен установить специальные линии связи между пятью локальными потребителями и новым сервером. Чтобы сократить затраты, руководство центра решило, что общая протяженность линий связи в сети должна быть минимальной. Хотя сервер может быть связан с каждым потребителем в отдельности, более экономичным было бы установить прямую связь с частью потребителей, а остальных связать с сервером через потребителей, которые уже получили эту связь (рис.2.10).

Рис.2.10

Шаг 1. Начинаем произвольно с любого узла и соединяем его с ближайшим узлом. Эти два узла теперь рассматриваются как связанные узлы, а остальные – как несвязанные узлы.

Шаг 2. Определяем несвязанный узел, который наиболее близок к одному из связанных узлов. Если два или более узлов можно рассматривать как ближайшие, то выбираем любой из них. Добавляем этот узел к связанным узлам. Повторяем этот шаг до тех пор, пока все узлы не станут связанными.

Используя жирные линии для пометки дуги, обеспечивающей соединение узлов, приходим к следующему результату, характеризующему шаг 1 (рис.2.11).

Рис.2.11

Повторение шага, заключающегося в добавлении ближайшего несвязанного узла к связанному сегменту сети (рис.2.12), дает нам решение задачи о дереве кратчайших расстояний, показанное на рис. 2.13.

Рис.2.12

Сумма расстояний в сети регионального центра составляет 110 км.

Рис.2.13

Заметим, что хотя дуги сети вычислительного центра измерялись в километрах, другие сетевые модели могут характеризоваться другими показателями – затратами, временем и т.д. В таких случаях алгоритм дерева кратчайших расстояний будет приводить к оптимальному решению (минимальные затраты, минимальное время и т.д.) применительно к рассматриваемому критерию.

Date: 2015-10-19; view: 2494; Нарушение авторских прав