Общие представления о фазовых пространствах

Состояние любого абстрактного объекта в науке можно описать двумя способами: аналитическим и графическим. Аналитический способ представляет объект с помощью уравнений, устанавливающих количественную причинно-следственную связь между характеристиками состояния объекта:

y = f (x₁, x₂, x₃ ….. x_n), (1.1)

где x₁, x₂, x₃ ….. x_n - параметры состояния объекта, играющие роль независимых и не связанных друг с другом причин; y - функция состояния объекта – представляющая собой следствие; f – неявная форма функциональной связи причин и следствия. Уравнение, устанавливающее аналитическую взаимосвязь всех параметров состояния в виде:

f (x₁, x₂, x₃ ….. x_n) = 0, (1.2)

называется уравнением состояния объекта.

Аналитический способ описания состояния объекта позволяет с любой заданной точностью определить значения его характеристик, однако требует затрат времени на решение уравнений, а значит, не обладает экспрессностью и наглядностью.

Графический способ позволяет более естественно, в привычных для человека пространственных образах, сразу представить все достижимые состояния объекта и их генезис. Однако для этого необходимо использовать не реальное, а фазовое пространство - пространство состояний объекта.

Фазовое пространство – это абстрактное пространство, в котором представляется в геометрических образах вся совокупность достижимых состояний объекта, а мерностями этого пространства являются параметры или другие характеристики объекта, однозначно определяющие его состояние: y; x₁…_.x_n.

В отличие от реального трехмерного пространства, в котором невозможно существование многомерных объектов, фазовое пространство – абстрактное пространство состояний. В зависимости от требований, которые предъявляются к полноте описания объекта, фазовое пространство может быть неограниченно мерным. Современные математические методы, разработанные в топологии (например, томография) и теории катастроф позволяют описывать и изображать многомерные объекты в виде двух- или трехмерных проекций.

Для получения фазового пространства необходимо выделить характеристики состояния объекта, которые исчерпывающе описывают состояния объекта (рис. 1.1) и поставить их во взаимно однозначное соответствие друг другу. В механике абстрактным объектом является материальная точка, параметрами состояния которой являются пространственные и временные характеристики, например амплитуда колебания x и скорость движения маятника 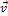, как это показано на рис. 1.2 для математического маятника. В термодинамике абстрактным объектом является система, характеристики состояния которой рассмотрены в разделе 1.2.

Фазовым портретом (или фазовой диаграммой состояния) объекта называется геометрический образ, представляющий всю совокупность достижимых состояний объекта в фазовом пространстве.

Из математики известно, что одинаковые по природе процессы описываются одинаковыми по своему характеру уравнениями и, наоборот, близость аналитических форм описания разных процессов указывает на их близкую природу. Это в полной мере относится к фазовым портретам и фазовым диаграмма состояния; одинаковый вид геометрического образа свидетельствует о близкой природе объектов и общности закономерностей причинно-следственных отношений, которыми они описываются.