
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Зависимость энергии Гиббса от состава
|
|
Условия фазового равновесия, сформулированные на предыдущем занятии для однокомпонентной системы, справедливы и для многокомпонентных систем. В основу алгоритма расчета фазовых равновесий с использование современных электронных баз данных положен поиск минимума энергии Гиббса. Алгоритм таких расчетом можно наглядно представить с помощью диаграмм Гиббса – Розебома, представляющих собой зависимость энергии Гиббса различных фаз бинарной системы от концентрации для разных температур.
Общей закономерностью формы самих кривых зависимости энергии Гиббса от концентрации является поведение их вблизи чистых компонентов. Оно вытекает из закона Рауля для разбавленных растворов и его следствия — закона Генри (в разбавленных растворах 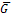 р-ра = RT∙ lnx + const). Используя формулу (1.6), получим выражение для изменения энергии Гиббса вблизи чистого компонента А (аналогичным оно будет и вблизи компонента B):
р-ра = RT∙ lnx + const). Используя формулу (1.6), получим выражение для изменения энергии Гиббса вблизи чистого компонента А (аналогичным оно будет и вблизи компонента B):
∆ G = (1- xB) 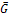 A + xB
A + xB 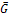 B = RT[(1- хВ)ln(1- xB) + xB ln xB] + xB∙ const. (3.1)
B = RT[(1- хВ)ln(1- xB) + xB ln xB] + xB∙ const. (3.1)
В пределе при xВ → 0∆ G → 0 (т.е. к величине энергии Гиббса компонента A в структуре рассматриваемой фазы). Тогда предельный наклон кривой ∆ G = f (x) равен:
 = μB – μA =
= μB – μA = 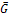 B -
B - 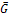 A = const + RT∙ ln
A = const + RT∙ ln  , (3.2)
, (3.2)
откуда следует, что при х B → 0  → ∞, т.е. кривая G(x) подходит кординатам компонентов снизу, с вертикальной касательной, как это показано на рисунке 3.1.
→ ∞, т.е. кривая G(x) подходит кординатам компонентов снизу, с вертикальной касательной, как это показано на рисунке 3.1.
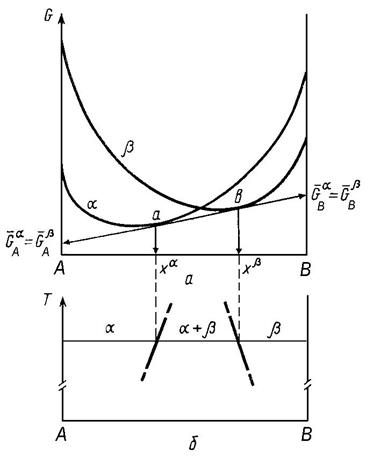
Рисунок 3.1. Геометрическая интерпретация условия равновесия фаз α и β
а – общая касательная к кривым G α и G β, б – соответствующий участок
фазовой диаграммы
Графическим образом условия равновесия двух и более фаз при данной температуре является касательная, проведенная к концентрационным зависимостям энергий Гиббса этих фаз (рисунок 3.1). Покажем это.
Из аналитической геометрии известно, что уравнение касательной ккривой G(х), проведенной в точке G°(хо), имеет следующий вид:
G = G°(хо) +  (x - xo). (3.3)
(x - xo). (3.3)
Найдя точки пересечения ее с ординатами компонентов, т. е. подставив х = 0и х = 1, с учетом (3.2) получим выражения, которые совпадают с выражением для химического потенциала идеального раствора:
μi - μi° = RT ∙ ln x i. (3.4)
Таким образом, точки пересечения касательной к кривой G(х) с осями ординат компонентов соответствуют парциальным энергиям Гиббса соответствующих компонентов в фазе состава, описываемого точкой, к которой проведена касательная.
Отсюда легко получается и условие равновесия фаз. Равенство химических потенциалов 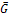 A α =
A α = 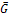 A βи
A βи  B α =
B α = 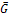 B β означает, что касательные к кривым G(х) обеих фаз пересекают ординаты обоих компонентов в одних и тех же точках; но прямые, имеющие две общие точки, совпадают. Следовательно, на геометрическом языке условие равновесия двух фаз α и β означает, что к кривым G α (х) и G 𝛽 (х) можно провести общую касательную, причем составы равновесных фаз определяются точками касания (рис. 3.1).
B β означает, что касательные к кривым G(х) обеих фаз пересекают ординаты обоих компонентов в одних и тех же точках; но прямые, имеющие две общие точки, совпадают. Следовательно, на геометрическом языке условие равновесия двух фаз α и β означает, что к кривым G α (х) и G 𝛽 (х) можно провести общую касательную, причем составы равновесных фаз определяются точками касания (рис. 3.1).
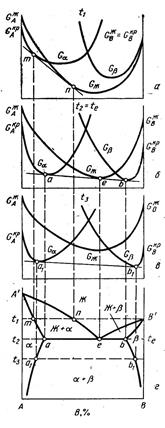
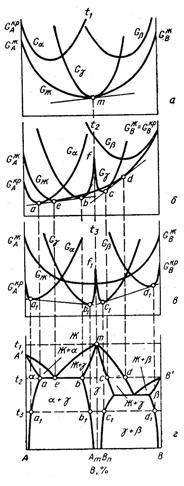
Рассмотрим для примера изменения вида диаграмм Гиббса - Розебома с температурой для системы с неограниченной растворимостью компонентов в жидком и твердом состояниях. Кривые зависимости энергии Гиббса от состава для жидких и твердых растворов этой системы при температурах t1 - t4 показаны на рис. 3.2, а - д.
При температуре t1 (рис. 3.2, а), совпадающей с температурой плавления более тугоплавкого компонента В, все сплавы находятся в жидком состоянии и кривая энергии Гиббса жидкого раствора Gж располагается ниже этой же кривой ∝-твердого раствора G 𝛼. Только на ординате компонента В кривые Gж и G 𝛼касаются одна другой в точке, отвечающей энергии Гиббса жидкого или твердого компонента В (поскольку при температуре плавления GЖВ = GкрВ). При температуре t2 (рис. 3.2, б) кривые энергии Гиббса Gж и G 𝛼пересекаются, в результате чего к ним можно провести общую касательную ab.
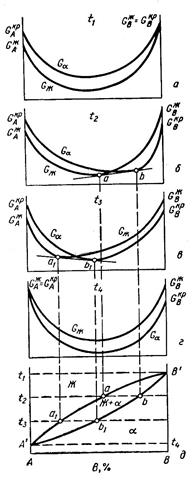
Рисунок 3.2. Зависимость энергии Гиббса жидкой фазы GЖ и α-твердого раствора G 𝛼 от состава системы с полной взаимной растворимостью компонентов в жидком и твердом состояниях
Точки а и b характеризуют соответственно составы жидкого Жa и твердого α b -pacтворов, которые оказываются в равновесии один с другим. В общем случае точки а и b не совпадают с точками минимума на кривых энергии Гиббса Gж и G α, так как условием равновесия двух фаз Жа и 𝛼b является не достижение минимума энергии Гиббса каждой фазы, а равенство химических потенциалов компонентов А и В вэтих фазах или первых производных энергии Гиббса по концентрации:
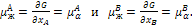 (3.3)
(3.3)
Отсюда следует, что через точки а и b можно провести общую касательную к кривым Gж и G 𝛼.
С понижением температуры до t3 (рисунок 3.2, в) точка пересечения кривых энергии Гиббса Gж и G 𝛼 смещается в сторону более легкоплавкого компонента А. Теперь к этим кривым можно провести другую касательную а1b1. Как и при температуре t2, точки а1 и b1 при температуре t3 характеризуют соответственно составы равновесных жидкого Ж a 1- и твердого 𝛼 b1 - растворов.
Наконец, при температуре t4 (рисунок 3.2, г), отвечающей температуре плавления компонента А, вся кривая энергии Гиббса G 𝛼оказывается ниже кривой G Ж и только на ординате этого компонента кривые G 𝛼и G Ж касаются одна другой (и ординаты) в точке, отвечающей энергии Гиббса компонента А (GЖВ = GкрВ).
Если точки, изображающие составы равновесных жидких и твердых растворов при разных температурах (а и b, а1 и b1 и др.), перенести на диаграмму в координатах состав – температура (рисунок 3.2, д), то построим диаграмму состояния, характерную для рассматриваемого случая взаимоотношений компонентов.
Возвращаясь к изотермам энергии Гиббса при температурах t 2 и t3, отметим, что при переходе от компонента А к компоненту В энергия Гиббса сплавов изменяется по линии, состоящей из трех участков — двух криволинейных участков в однофазных областях Ж и α и прямолинейного участка в двухфазной области Ж + 𝛼.
3.2.Твердые растворы: условия их образования и распада.
Для обеспечения полной взаимной растворимости компонентов в бинарной системе, т.е. образования непрерывного ряда твердых растворов во всем интервале концентраций (рис. 3.2, д; рис. 3.3.I, д) необходимо соблюдение трех обязательных условий.
1. Непрерывными могут быть только твердые растворы замещения. Для реализации этого условия необходимо, чтобы кристаллические решетки компонентов А и В имели одинаковый тип кристаллической решетки, т.е. были изоструктурны. Изоструктурность следует рассматривать как необходимое условие полной взаимной растворимости (изоморфизма) компонентов в твердом состоянии.

I) II)
Рисунок 3.3. Диаграммы Гиббса – Розебома для системы с полной взаимной растворимостью компонентов в жидком и твердом состояниях и минимумом на ликвидусе и солидусе - I) и системы с эвтектическим равновесием - II)
Два следующих фактора следует рассматривать как достаточные для образованиятвердых растворов.
2. Размерный фактор атомные или ионные радиусы замещающихся частиц кристаллической решетки должны быть близки. Как правило, различия в их размерах не должно превышать 10÷15 %.

I) II)
Рисунок 3.4. Диаграммы Гиббса – Розебома для систем с перитектическим
равновесием (I) и образованием конгруэнтно плавящегося соединения (II).
3. Фактор химической связи. Замещающиеся составляющие кристаллической решетки должны иметь аналогичное электронное строение, близкий эффективный заряд атомов и образовывать подобный характер химической связи в аналогичных соединениях. Несмотря на то, что последнее условие имеет качественный характер, оно может играть решающую роль при образовании твердых растворов в неметаллических системах, образующихся за счет ковалентных или, ионно-ковалентных связей.
Контрольные вопросы
1. Как измениться вид уравнения правила фаз Гиббса для двухкомпонентной системы? Какие возможности имеются в двухкомпонентной системе для повышения устойчивости состояния равновесия?
2. На диаграммах Гиббса – Розебома, представленных на рисунках 3.3 и 3.4 укажите геометрические образы, соответствующие уравнению фазового равновесия: μ(1) = μ(2).
3. Как изменяется положение концентрационной зависимости энергии Гиббса с повышением температуры?
Геометрические образы моно- и нонвариантных фазовых равновесий в двухкомпонентных системах. 4.2. Сложные диаграммы состояния бинарных систем.
Геометрические образы моно- и нонвариантных фазовых
Date: 2015-10-18; view: 3724; Нарушение авторских прав