Системная интерпретация

Аксиоматики геометрии

Эвклидова пространства

Аксиоматика эвклидовой геометрии в интерпретации Д.Гильберта в качест-ве основных элементов эвклидова про-странства принимает понятия «точка», «прямая» и «плоскость», а основных отношений - «инцидентность», «между» и «движение» [1]. Ниже следуют тради-ционные и системные толкования и оп-ределения этих понятий.

Точка

«Точка есть то, что не имеет частей»

или «…точка есть то, часть него есть ничто» (Эвклид). Но ведь всякий ре-альный объект, являясь системой, име-ет части, из которых он состоит. Поэто-му точку можно понимать как предел, к которому стремится какое-либо тело в абстрактном процессе бесконечного уменьшения его размеров. И этот про-цесс не может быть завершен, так как в

«малом не существует наименьшего, но всегда есть еще меньшее» (Анаксогор)

[48]. Отсюда следует, что пространст-

во бесконечно не только вовне, но и во-

внутрь в любой своей малой части. Практически приемлемо следующее

определение точки: «… тела дальней-

Рис. 5.5. Точка А

Рис.5..6. Точка А - начало луча а

Рис.5.7. Точки А и В – концы отрезка

АВ прямой линии а

Рис.5.8. Точка А – центр связки

прямых

Рис.5.9. Графическая точка А как

результат наложения линии а на

линию b

Рис.5.10. Точка А – результат

пересечения прямой а с плоскостью a

Ри с.5.11. Точка А – результат пересе-

чения линии а с поверхностью Ф

Рис.5.12. Точка А – результат

пересечения трёх плоскостей

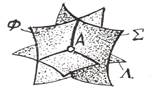
Рис.5.13. Точка А – результат

пересечения трёх поверхностей

шее деление которых невозможно в

в пределах наблюдения, называются

точками» [ 48].

По ассоциации с этими определе-ниями понятие о точках можно уподо-бить понятию об «атомах» как об изна-

чально неделимых частицах, из кото-рых состоит вещество.

Определение 5.1 Точка есть эле-ментарная (неделимая) нульмерная геометрическая частица (рис.5.5).

Конструктивно точкой является на-чало луча а (рис.5.6), конец А или В от-резка АВ линии а (рис.5.7), результат пересечения двух линий на поверхнос-ти, (плоскости) (рис.5.9), одной линии с поверхностью (плоскостью) (рис.5.10, 5. 11), 3-х поверхностей (плоскостей) меж-ду собой. (рис.5.12, 5.13). Эвклид опре-делил точку конструктивно как конец линии.

В отличии от геометрического поня-

тия точки понятие графической точки означает фигуру наложения ширины одной линии на ширину другой. Чем то-ньше пересекающиеся линии, тем кон-кретней графическая точка, которая, как правило, изображается на геометричес-ких чертежах кружочком диаметром 1 – 1,5 мм, центром которого является ре-зультат пересечения продольных осей «полос» пересекающихся линий.

В графической работе точка пере-сечения двух линий получается тем то-чнее, чем ближе к прямому углу распо-лагаются эти линии.

Определение 5.2. Пространство, элементами которого являются точ-ки, называется т о ч е ч н ы м.

Такое пространство дискретно и представляется некоторым бесконеч-ным множеством точек. Для того, чтобы определить «мощность» этого множест-ва, одну из его точек принимают за на-чало отсчёта, через которое проходят три взаимно-перпендикулярные направ-ления, относительно которых положе-ние каждой точки в пространстве опре-деляется тремя декартовыми координа-тами или тремяпараметрами. Поэтому

такое множество называют трёхпара-метрическим и обозначают символом ¥³. Трёхпараметричность точечного

пространства определяет его тре мер- ность, так как параметры положения каждой его точки суть меры её откло- -

нения (правее, левее), удаления (бли-

же, дальше) и возвышения (выше, ни-

же) относительно начала отсчета.

Линия

«Линия есть длина без ширины» (Эвклид). Такое понятие линии возник-ло из первоначального назначения гео-метрии как землемерия. Основной опе-рацией было измерение расстояний шагами или верёвками. Эти измерения через абстракцию привели к понятию длины. Установление точных границ зе-мельных участков, требующее сужения пограничной черты, привело к понятию линии, не имеющей ширины.

Определение кратчайших расстоя-ний между двумя точками с помощью натянутой нити, размышления над гео-метрией солнечных и «зрительных» лу-чей привело к понятию прямой линии.

Прямая занимает особое положе-ние среди остальных линий. Она зада-ётся двумя несовпадающими точками пространства и может быть продолжена в обе стороны до бесконечности. При этом она «проходит» через однопара-метрическое множество (¥¹) точек про-странства, принадлежащих этой пря-мой.

Если все точки пространства попар-но соединить прямыми, то оно станет называться линейчатым. Каждая точка исходного точечного пространства в процессе его преобразования в линей-чатое соединяется прямыми линиями со всеми остальными его точками, ста-новясь центром пространственной связ-ки прямых (рис.5.4), заполняющих всё пространство. Это пространство четы-рёхпараметрично, так как пар точек, оп-ределяющих эти прямые в простран-стве - ¥⁶ , а на каждой прямой их ¥².

Понятие связки как двупараметри-ческого множества прямых, проходя-щих через одну точку в пространстве, относится к числу фундаментальных в геометрии (рис.5.4).

Представление линии как однопа-раметрического множества точек может быть заменено более наглядным дина-

мичным представлением её как траек-

тории непрерывно движущейся точки. Такое кинематическое представление

линии более естественно, так как оно

Рис.5.14. Отрезок АВ прямой а

Рис.5.15. Две полупрямые или два луча

Рис.5.16. Пространственная ломаная линия

Рис.5.17. Пространственная кривая линия

Рис.5.18. Прямая линия а как результат пересечения двух плоскостей.

Рис.5.19. Плоская ломаная линия как результат пересечения плоскости и многогранной поверхности

Рис.5.20. Плоская кривая линия как

результат пересечения плоскости и

кривой поверхности

моделирует естественный процесс её

образования. И действительно, кончик

пера или карандаша (как точка), пере-

мещаясь в двумерном пространстве листа бумаги, выделяет в нём те точки, непрерывное множество которых обра-зует их систему, называемую линией.

Определение 5.3. Линией называ-ется одномерная система последова-тельных положений точки, движущей-ся в пространстве

Если элементами линии как систе-мы являются точки, то в качестве свя-зей между ними выступает отношение их принадлежности к ней. Поэтому ли-нию можно определить как систему принадлежащий ей точек.

Точки, принадлежащие прямой ли-нии, называются коллинейными. Отсю-да следует

Определение 5.4. Прямой линией называется система коллинейных то-чек.

Из непрерывности движения точки следует свойство непрерывности обра-зуемой ею линии.

Совокупность последовательных по-ложений точки, движущейся в простран-стве по определённому закону, назы-вают геометрическим местом точек.

Всё черчение и рисование суть ки-нематические процессы получения раз-личных линий.

Определение 5.5. Часть прямой линии с, заключенной между её несов-падающими точками А и В, называет-ся о т р е з к о м АВ прямой с (рис.5.14).

Если на прямой а взять одну точку А, то она разобьёт прямую на две полу-прямые или два луча, дополнительные друг к другу (рис.5.15). При этом точка А называется начальной.

Если произвольные точки простран-ства соединить отрезками прямых, то образуется пространственная ломаная

линия (рис.5.16). Соединяемые точки называют вершинами ломаной, а пря-молинейные отрезки между ними,- её звеньями. Ломаная линия может быть замкнутой или разомкнутой.

Если произвольные точки простран-ства соединить плавным и непрерыв-ным движением точки, то полученная линия будет пространственной кривой.

(рис.5.13).

Во всякую кривую линию можно

вписать ломаную, последовательно со-

единив отдельные её точки отрезками

прямых. Поэтому можно сказать, что всякая кривая линия имеет свой много - угольный прототип.

Подчиняя движущуюся точку раз-личным законам движения, можно об-разовать множество кривых линий.

Кривые линии подразделяются на плоские и пространственные, законо-мерные и незакономерные. Закономер-ные, в свою очередь, делятся на алгеб-раические и трансцендентные, описы-ваемые, соответственно, алгебраичес-кими и тригонометрическими уравнени-ями. По степени уравнения судят о по-рядке алгебраической кривой.

Графически порядок алгебраичес-кой кривой можно определить по макси-мальному числу точек её пересечения с прямой линией.

Незакономерные линии конструиру-ются по наперед заданным условиям или рисуются по «замыслу архитекто-ра».

Конструктивно линия может быть получена как результат пересечения 2-х

плоскостей (рис.5.18), плоскости и повер-хности (рис.5.19, 5.20) и двух поверхностей (рис. 5.21, 5.22).

Две плоскости пересекаются по

п р я м о й линии, плоскость и много-гранная поверхность, - по плоской л о –

м а н о й линии, плоскость и кривая поверхность, - по плоской к р и в о й линии, две многогранные поверхности – по п р о с т р а н с т в е н н о й л о м а- н о й линии и две кривые поверхнос-ти – по п р о с т р а н с т в е н н о й к р и в о й линии.

В архитектуре и дизайне наиболее распространенными являются прямые и плоские кривые линии.

Date: 2015-10-18; view: 512; Нарушение авторских прав