Свойства отношений, порождаемых группой III аксиом конгруэнтности (движения)

Основным содержанием 10 аксиом III группы является фундаментальное понятие геометрического движения и порождаемых им отношений конгруэнт-ности (одинаковости, равенства), а также перпендикулярности элементов эвклидова пространства.

Определение 5.30. Геометричес-ким движением называется такой про-цесс, при котором точкам А, В, С, …, прямым а, b, c,…, плоскостям a, b, g, … в пространстве R соответствуют точки А¢,В¢,С,…, прямые а¢, b¢, с¢,… и плоскости a¢, b¢, g.¢ этого же прост-ранства.

При этом говорят, что такое движе-ние устанавливает «преобразование пространства в себя».

К числу основных свойств геомет-рического движения относятся его спо-собность сохранять отношение инциде-нтности и отношения порядка «между» в процессе преобразования исходных элементов пространства в им соответ-ственные.

Если движение соотносит точкам и прямым плоскости их же самих, то пре-образование, осуществляемое таким движением называется тождествен-ным. При этом говорят, что такое пре-образование оставляет неподвижными

все элементы плоскости.

Определение 5.31. Конгруэнтнос - тью называется отношение одинако-вости по форме между элементами одной размерности, когда их движени-ем можно привести в тождественное расположение (рис.5.71, а, б, в).

Определение 5.32. Равенством называется отношение конгруэнтнос-ти между элементами одной размер-ности, характеризующее их метри-ческую одинаковость.

Все конгруэнтные элементы метри-чески равны друг другу.

Из свойств движения и конгруэнт-ности выводятся понятия о таких геоме-трических системах как фигуры, треу-гольники равносторонние и равнобед-ренные, плоские смежные, вертикаль-ные и прямые углы, их поперечины, перпендикуляры к прямым и плоскос-тям, середины отрезков, медиатрисы, биссектрисы плоских углов, внутрен-ние и внешние острые, прямые и ту-пые углы треугольников, их чевианы, высоты, медианы, медиатрисы и бис-сектрисы.

Их системные определения:

Определение 5.33. Плоской фиг-урой называется система компланар-ных точек и линий;

Определение 5.34. Равносторон- ним называется треугольник с конгру-энтными сторонами; -

Определение 5.35. Равнобедрен-ным называется треугольник с двумя конгруэнтными сторонами;

Определение 5.36. Развернутым называется угол, стороны которого образуют один отрезок;

Определение 5.37. Настоящим или неразвёрнутим называется угол, стороны которого лежат по одну сторону по отношению друг к другу;

Определение 5.38. Смежным на-зывается угол, дополнительный к дан-ному до развернутого;

Определение 5.39. Накрестлежа-щим называется угол, образованный продолжениями сторон данного угла;

Определение 5.40. Поперечиной угла называется отрезок с концами на его сторонах;

Рис.5.72. Чевианы произвольного треугольника

Рис.5.73. Медианы и медиатрисы произвольного треугольника.

Точка пересечения медиан –

центр тяжести треугольника.

Точка пересечения медиатрис – центр

окружности, описанной вокруг треугольника

Рис.5.74. Высоты и биссектрисы произвольного треугольника.

Точка пересечения высот –

- ортоцентр треугольника.

Точка пересечения биссектрис – центр

окружности, вписанной в треугольник

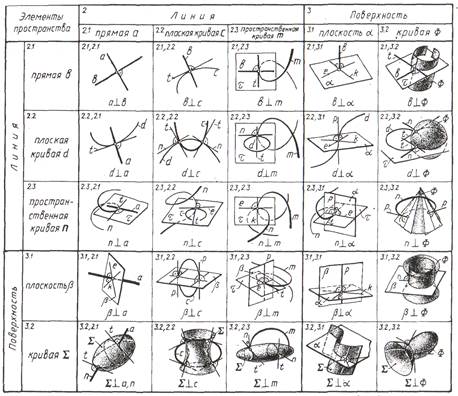
Рис.5.75. Таблица вариантов перпендикулярности элементов

эвклидова пространства

Определение 5.41. Прямым назы- вается угол, равный смежному;

Определение 5.42. Острым назы-вается угол, меньший прямого;

Определение 5.43. Тупым называ-ется угол, больший прямого;

Определение 5.44. Взаимно пер-пендикулярныи называются прямые, инцидентные сторонам прямого угла;

Определение 5. 45. Перпендикуля-ром к плоскости называется прямая, перпендикулярная к двум её конкурент-ным прямым;

Определение 5.46. Серединой от--резка называется точка, равноудалён-ная от её концов;

Определение 5.47. Медиатриссой

отрезка называется прямая, перпенди-

кулярная к нему в его середине;

Определение 5.49. Биссектрисой линейного угла называется прямая, де-лящая его на два конгруэнтных угла;

Определение 5.50. Внутренними называются углы треугольника, обра-зуемые его сторонами.

Определение 5.51. Внешними назы ваются углы треугольника, смежные его внутренним углам;

Определение 5. 52. Прямоуголь-ным называется треугольник с одним

прямым внутренним углом.

Определение 5.53. Тупоугольным называется треугольник с одним ту-пым внутренним углом;

Определение 5.54. Чевианами треугольника называются три луча с началами в его вершинах, инцидент-ные его произвольной внктренней точке и конкурентные со сторонами, противолежащими этим вершинам.

Определение 5.55. Медианами

треугольника называются чевианы, проходящие через середины его сто-рон (рис.5.73);

Определение 5.56. Медиатрисами треугольника называются его попере-чины, перпендикулярные к серединам его сторон .( рис.5.73).

Определение 5.57. Высотами треугольника называются чевианы, перпендикулярные к его сторонам.

Определение 5.58. Биссектрисами треугольника называются чевианы, делящие его внутренние углы попо-

лам (рис.5.74);

Определение 5.58. Перпендикуляр-ностью называется пересекаемость

элементов одинаковой или разной раз-мерности под прямым углом.

Это чрезвычайно важная связь ме-

Рис. 5.76. Конгруэнции нормалей к поверхностям:

а – сферической,

б - цилиндрической;

в – конической.

Рис. 5.77. Конгруэнция нормалей поверхности вращения Ф и её

фокальная поверхность S

Рис 5.78. Ортогонально сопряженные

софокусные кривые:

а – эллипсы и гиперболы;

б – параболы

жду элементами пространства, из кото-

рых создаются искусственные системы, ибо, по словам Ле Корбюзье «…прямой угол – это необходимый и достаточный

инструмент для работы, поскольку с его помощью можно самым точным обра-зом отмерить пространство» [ 58].

Так как перпендикулярность являет-ся пересекаемостью, то, связывая два элемента в их систему, она порождает третий, им инцидентный двойной эле-мент, размерность которого на единицу ниже, чем наименьшая размерность со-единяемых элементов (рис.5.75).

Перпендикулярность двух любых элементов пространства взаимна.

Две прямые перпендикулярны в 2-х случаях: когда они компланарны и меж-ду ними угол 90° (рис.5.75, п.2.1,2.1); когда одна прямая принадлежит плос-

кости, перпендикулярной ко второй пря-мой. В этом случае обе прямые скрещи-ваются под прямым углом.

Прямая b перпендикулярна к плос-кой кривой с (рис.5.75, п. 2.1,2.2) или к пространственной кривой m (рис.5.75, п. 2.1,2.3) в их обыкновенных точках, если она является их нормалью в этих точ-ках.

Прямая b перпендикулярна к плос-кости a, если она перпендикулярна к двум её конкурентным прямым(рис.5.75, п.2.1,3.1).

Прямая b перпендикулярна к повер-хности Ф в её обыкновенной точке, если она является нормалью этой поверхно-сти в этой точке (рис.5.75, п.2.1,3.2).

Теоретический и практический ин-терес представляют многообразия нор-малей к различным поверхностям.

Так как к кривой поверхности в каж-дой её обыкновенной точке можно про-вести одну нормаль, то совокупность всех нормалей к поверхности представ-ляет их двупараметрическое множество (по количеству точек), называемое кон-

груэнцией нормалей [27], (рис.5.71).

Конгруэнцией нормалей сферы яв-ляется связка её радиальных лучей;

Конгруэнцией нормалей поверхнос-ти прямого кругового цилиндра явля-ется однопараметрическое множество пучков радиусов его нормальных сече-ний (рис.5.76, б). Такая конгруэнция на-зывается ортогональной [ 27].

Конгруэнцией нормалей поверхнос-ти конуса вращения является однопа-

-раметрическое множество образующих

соосных конических поверхностей, пер-пендикулярных к образующим данной

поверхности в точках на её параллелях (рис.5.76, в).

Конгруэнцией нормалей поверхнос-ти вращения является однопарамет-рическое множество касательных к не-которой поверхности S, образованной

вращением эволюты меридиана данной поверхности (рис.5. 77).

Поверхность, касательные к кото-рой являются нормалями данной пове-рхности, называется фокальной [8].Она является геометрическим местом цен-тров кривизн в точках данной поверхно-сти (рис.5.77)

Если в конгруэнции нормалей «по-гружать» те или иные линии, то они «выделят» из этих конгруэнций пере-секающие их нормали, которые в своей совокупности образуют те или иные поверхности.

Две плоские кривые с и d взаимно пер-пендикулярны, если они компланарны и в точках пересечения касательны ко взаимно перпендикулярным прямым t и n (рис.5. 75, п. 2.2,2.2)

Если две точки плоскости принять за фокусы семейств эллипсов и ги-пербол, то эти софокусные линии обра-зуют взаимно-ортогональные семейст-ва кривых (рис.5.78). Так расположен-ные линии называются ортогонально сопряжёнными.

Две плоские кривые m и n имеют взаимно перпендикулярные направле-ния, если они лежат во взаимно-пер-пендикулярных плоскостях a и b и ка-сательны к компланарным с ними пря-мым a, b, c и d, перпендикулярным к линии пересечения плоскостей a и b (рис. 5.79). Так расположены эллипти-ческие звенья различных цепей.

Плоская кривая d перпендикулярна к пространственной кривой m в обык-новенной точке, если она лежит в со-прикасающейся плоскости t и каса-тельна к нормали n пространственной кривой (рис.5.75, п.2.2,2.3).

Плоская кривая d перпендикулярна к плоскости a, если она касательна к

нормали n плоскости a в её основании

Рис. 5.79. Взаимно перпендикулярные эллипс и гипербола

Рис.5.80. Ортогонально-сопряженная сеть пространственных линий на поверхности трёхосного эллипсоида

Рис.5.81. Различные условия

взаимной перпендикулярности

двух плоскостей

(см. рис.5.75, пп. 2.2,3.1; 3.1,2.2)

Плоская кривая d перпендикулярна к поверхности вращения, если она ком-планарна с нормальным (рис.5.75, п. 2.2,3.2) или меридиональным (п.3.2,2.2)

сечением поверхности и ортогонально

сопряжена с ним.

Две пространственные кривые m и n взаимно перпендикулярны, если в то-чке пересечения они имеют общую со-прикасающуюся плоскость t и касате-льны к лежащим в этой плоскости двум взаимно перпендикулярным прямым l и k (см. рис.5.75, п.2.3,2.3).

Пространственные кривые взаимно перпендикулярны, если они образуют линейный каркас ортогонально сопря-женных линий криволинейчатой поверх-ности (рис.5.80).

Пространственная кривая n перпен-дикулярна к плоскости a, если в точке её пересечения с этой плоскостью она касательна к прямой l соприкасающейся плоскости t, перпендикулярной к плос-кости a (рис.5.75, п. 2.3,3.1).

Пространственная кривая n перпен-дикулярна к кривой прямолинейчатой поверхности Ф (п. 2.3,3.2) или поверх-ности вращения S (п. 3.2,2.3), если в точках её пересечения с ними она ка-сательна к нормалям к этим поверх-ностям.

Плоскость a перпендикулярна плос-кости b при следующих условиях:

условие 1 – если плоскость a про-ходит через перпендикуляр к плоскости b (рис.5.75, п.3.1, 3.1);

условие 2 –если плоскость a парал-лельна перпендикуляру к плоскости b (рис.5.81, а);

условие 3. – если плоскость a перпендикуляра к прямой а, принадле-жащей плоскости b (рис.5.81, б);

условие 4 – если плоскость a пер-пендикулярна к прямой а, параллельной плоскости b (рис.5.81, в).

Плоскость b перпендикулярна к по-верхности вращения, если она проходит через нормаль к поверхности перпенди-кулярно к оси её вращения (рис.5.75, п.3.1, 3.2).

Плоскость a перпендикулярна к ци-линдрической поверхности, если она перпендикулярна к её образующим. Се-чение поверхности такой плоскостью называется нормальным (рис.5.75,п.3.2, 3.1).

По виду нормального сечения су-дят о характере поверхности.

Две поверхности Ф и S взаимно перпендикулярны, если они образова-ны вращением ортогонально сопряжен-ных плоских кривых вокруг их действи-тельной оси (рис.5.75, п. 3.2,3.2) или соответственные элементы линейных каркасов этих поверхностей ортогона-льно сопряжены (рис.5.82)

Рис.5.82. Ортогонально-сопряженные поверхности трёхосного эллипсоида, одно- и двуполостных эллиптических гиперболоидов

Date: 2015-10-18; view: 399; Нарушение авторских прав