Решение игр в смешанных стратегиях

Если игра не имеет седловой точки, то применение чистых стратегий не даёт оптимального решения игры. В таком случае можно получить оптимальное решение, случайным образом чередуя чистые стратегии.

Смешанной стратегией S_A игрока А называется применение чистых стратегий А₁, А₂,..., А_i,..., А_m с вероятностями р₁, р₂,..., р_i,..., p_m, причём . Смешанные стратегии игрока А записываются в виде матрицы

,

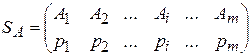или в виде строки .

Аналогично для игрока В

,

или , где .

На основании принципа минимакса определяется оптимальное решение игры: эта пара оптимальных стратегий в общем случае смешанных, обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не выгодно отступать от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры v. Цена игры удовлетворяет неравенству

α ≤ v ≤ β (7.6)

Справедлива основная теорема теории игр – теорема Неймана: каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно, среди смешанных стратегий.

Пусть 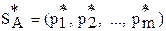и – пара оптимальных стратегий. Если чистая стратегия входит в оптимальную смешанную стратегию с отличной о нуля вероятностью, то она называется активной.

Справедлива теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остаётся неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий.

Эта теорема имеет большое практическое значение, она даёт конкретные модели нахождения оптимальных стратегий при отсутствии седловой точки. Чем больше размерность матрицы, не содержащей седловой точки, тем сложнее решение. Поэтому в теории матричных игр рассматриваются способы, с помощью которых решение одних игр сводится к решению других, более простых (в частности с помощью сокращения размерности матрицы). Сократить размерность матрицы можно, исключая дублирующие и заведомо невыгодные доминирующие стратегии. Например, в матрице P₂ для игрока В заведомо невыгодной является четвёртая стратегия, так как все значения а_i4 превышают соответствующие значения элементов первого и второго столбца. Четвёртый столбец матрицы можно исключить (игрок В не воспользуется этой стратегией).

Можно сократить размер матрицы, разбив её на подматрицы, в которых суммы элементов по столбцам и строкам равны. Тогда вместо чистых стратегий в матрицу включаются смешанные. Элементы сокращённой матрицы получаются делением соответствующих сумм элементов на число чистых стратегий. Если смешанные стратегии входят в число оптимальных, то вероятности использования входящих в них чистых стратегий равны между собой.

Пример 7.2. Сократить размерность матрицы

Решение. В матрице P₃ для подматриц выполняется условие равенства сумм элементов по строкам и столбцам. Объединяя стратегии А₁ А₂ А₃; А₄ А₅; В₁ В₂; В₃ В₄, получим

Полученная матрица содержит седловую точку

α = β = 1 = а₁₁.

Поэтому решение первоначальной игры, заданной матрицей P₃, имеет вид , , 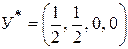т.к. стратегии А₁, А₂, А₃ для игрока А и стратегии В_1, В₂ для игрока В чистые и равноправные. Стратегии А₄, А₅ и В₃, В₄ не применяются. Цена игры равна 1. Оптимальной для игрока А является комбинация стратегий А₁, А₂, А₃, а для игрока В – комбинация стратегий В₁ и В₂. Вероятность применения стратегий А₁, А₂ и А₃ равны между собой (Σ р_i = 1). Аналогично для второго игрока, Σ q_j = 1.

Рассмотрим простейший случай конечной игры 2х2, в которой каждый игрок имеет две стратегии. Платёжная матрица игры Если такая игра имеет седловую точку, то оптимальное решение – это пара чистых стратегий, соответствующих этой точке. При отсутствии седловой точки игра в соответствии с основной теоремой теории игр имеет оптимальное решение, определяемое парой смешанных стратегий и .

Для того чтобы их найти, воспользуемся теоремой об активных стратегиях. Если игрок А придерживается своей оптимальной стратегии , то его средний выигрыш будет равен цене игры v при любой активной стратегии игрока В. Для игры 2х2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Выигрыш игрока А (проигрыш игрока В) – случайная величина, математическое ожидание (среднее значение) которой является ценой игры. Поэтому средний выигрыш игрока А (оптимальная смешанная стратегия) будет равен v и для первой и для второй стратегий.

Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию , а игрок В – чистую стратегию В₁ (это соответствует первому столбцу матрицы Р), равен цене игры v:

.

Тот же средний выигрыш получит игрок А, если 2-й игрок применяет стратегию В₂, т.е. . Учитывая, что , получаем систему уравнений для определения оптимальной стратегии и ценой игры v:

(7.7)

Решая эту систему, получим оптимальную стратегию

, (7.8)

и цену игры

. (7.9)

Составляя аналогичную систему уравнений, можно найти оптимальную стратегию для игрока В:

. (7.10)

Пример 7.3. Найти решение игры, заданной матрицей .

Решение. Матрица не имеет седловой точки. По формулам (7.8 – 7.11) находим оптимальные стратегии и цену игры:

Date: 2015-10-18; view: 844; Нарушение авторских прав