
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Глава 7. Элементы теории игр
|
|
7.1 Основные понятия теории игр
Теория игр – это теория математических моделей ситуаций, интересы участников которых различны, причём они достигают своей цели различными путями. Столкновение противоположных интересов участников приводит к возникновению конфликтных ситуаций.
Задачей теории игр является выработка рекомендаций по рациональному образу действия участников конфликта.
Игрой называется упрощённая модель конфликтной ситуации.
Например, шахматы, шашки, карточные игры – естественная база для анализа конфликтных ситуаций.
Терминология теории игр: игроки (стороны, участвующие в конфликте), выигрыш (исход конфликта) и т.д.
Игры бывают:
- комбинаторные (шахматы);
- азартные (кости, рулетка, герб – решка);
- стратегические (источник неопределённости – отсутствие информации о действиях противника).
Рассмотрим стратегические игры. Стратегические игры бывают парными (два игрока) и множественными. Большое практическое значение имею парные игры. Обозначим участников игры через А и В.
Для каждой формализованной игры вводятся правила, т.е. система условий, определяющая: 1) варианты действий игроков; 2) объём информации каждого игрока о поведении партнёров; 3) выигрыш, к которому приводит каждая совокупность действий. Результат игры (выигрыш) определяется некоторым числом.
Игра называется игрой с нулевой суммой, или антагонистической, если выигрыш одного из игроков равен проигрышу другого. Если обозначить а – выигрыш одного из игроков, b – выигрыш другого, то для игры с нулевой суммой b = – a, поэтому достаточно рассматривать, например, а.
Ходом в теории игр называется выбор и осуществление одного из предусмотренных правилами действий. Ходы могут быть личными и случайными. Личный ход – это сознательный выбор игроком одного из возможных действий (например, ход в шахматной игре). Случайный ход – это случайное выбранное действие (например, выбор карты из перетасованной колоды). В дальнейшем будем рассматривать только личные ходы игроков.
Стратегией игрока называется совокупность правил, определяющих выбор его действий при каждом личном ходе в зависимости от сложившейся ситуации.
Игрок принимает решения по ходу игры. Теоретически можно предположить, что эти решения приняты игроком заранее. Это означает, что игрок выбрал определённую стратегию, которая может быть задана в виде списка правил или программы.
Игра называется конечной, если у каждого игрока имеется конечное число стратегий и бесконечной – в противном случае.
Оптимальной называется стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный выигрыш, когда второй игрок придерживается своей стратегии; или второй игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии.
Оптимальные стратегии должны удовлетворять условию устойчивости, т.е. любому из игроков должно быть невыгодно отказаться от своей стратегии в этой игре.
Если игра повторяется многократно, то игроков может интересовать не выигрыш и проигрыш в каждой конкретной партии, а средний выигрыш (проигрыш) во всех партиях.
Целью теории игр является определение оптимальной стратегии для каждого игрока.
Важнейшее ограничение теории игр – единственность выигрыша как показателя эффективности, в то время как большинство реальных экономических задач имеет более одного показателя эффективности. Кроме того, в экономике, как правило, возникают задачи, в которых интересы партнёров не обязательно антагонистические.
7.2 Платёжная матрица. Нижняя и верхняя цена игры
Рассмотрим парную конечную игру. Пусть игрок А располагает m личными стратегиями А1, А2,..., Аm, а игрок В имеет n личных стратегий В1, В2,..., Вn. В этом случае говорят, что игра имеет размерность m х n. В результате выбора игроками любой пары стратегий Аi и Bj (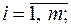
 ) однозначно определяется исход игры, т.е. выигрыш aij игрока А (положительный или отрицательный) и проигрыш (– aij) игрока В. Предположим, что значения aij известны для любой пары стратегий (Аi; Bj)
) однозначно определяется исход игры, т.е. выигрыш aij игрока А (положительный или отрицательный) и проигрыш (– aij) игрока В. Предположим, что значения aij известны для любой пары стратегий (Аi; Bj)
Матрица 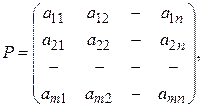 элементами которой являются выигрыши, соответствующие стратегиям Аi и Bj, называется платёжной матрицей или матрицей игры. Общий вид этой матрицы представлен в таблице 7.1.
элементами которой являются выигрыши, соответствующие стратегиям Аi и Bj, называется платёжной матрицей или матрицей игры. Общий вид этой матрицы представлен в таблице 7.1.
Таблица 7.1 – Платёжная матрица
| Вj Аi | В1 | В2 | ... | Вn |
| A1 | a11 | a12 | … | a1n |
| A2 | a21 | a22 | … | a2n |
| … | … | … | … | … |
| Am | am1 | am2 | … | amn |
Строки этой таблицы соответствуют стратегиям игрока А, а столбцы – стратегиям игрока В.
Пусть игрок А выбирает некоторую стратегию Аi, тогда в наихудшем случае (например, если выбор станет известным игроку В) он получит наименьший выигрыш 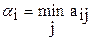 . (7.1)
. (7.1)
Предвидя такую возможность, игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш.
 (7.2)
(7.2)
Величина α – гарантированный максимальный выигрыш игрока А, называется нижней ценой игры или максимином.
Стратегия, соответствующая максимуму, называется максиминной стратегией. Игрок В, выбирая стратегию, исходит из следующего: при выборе некоторой стратегии Вj, его проигрыш не превысит максимума из значений элементов j-го столбца матрицы.
 . (7.3)
. (7.3)
Рассматривая множество βj для различных значений j, игрок В выберет такое значение j, при котором его максимальный проигрыш минимизируется.
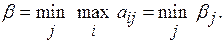 (7.4)
(7.4)
Величина β называется верхней ценой игры, или минимаксом. Это гарантированный минимальный проигрыш игрока В.
Стратегия, соответствующая минимаксу, называется минимаксной стратегией.
Если α = β = v, (7.5)
то выигрыш игрока А – вполне определённое число, игра называется вполне определённой, а выигрыш v (7.5) называется ценой игры и равен элементу матрицы, который одновременно является наибольшим в своём столбце и наименьшим в своей строке. Этот элемент называется седловой точкой (по аналогии с поверхностью седла, которая искривляется вверх в одном направлении и вниз в другом).
Седловой точке соответствуют вполне определённые (чистые) стратегии игроков. Совокупность чистых стратегий А* игрока А и В* игрока В называют решением игры, которое обладает следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то для другого отклонение его от его оптимальной стратегии не может быть выгодно.
Пример 7.1. Определить нижнюю и верхнюю цены для игр, заданных платёжными матрицами
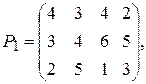

Решение. Все расчёты удобно проводить в таблице, в которой кроме матрицы Р введены столбец αi и строка βj (табл. 7.2) и (табл. 7.3).
Таблица 7.2 – Платёжная матрица Р1′ Таблица 7.3 – Платёжная матрица Р2′
| Вj Аi | В1 | В2 | В3 | В4 | αi |
| A1 |  2 2
| ||||
| A2 | |||||
| A3 | |||||
| βj |  6 6
|
| Вj Аi | В1 | В2 | В3 | В4 | αi |
| A1 | |||||
| A2 |  2 2
| ||||
| A3 | – 1 | –1 | |||
| βj |  2 2
|
Решение. Минимальные значения aij в строках матрицы Р1 равны соответственно (2, 3, 1). Максимальное значение из них равно 3. Следовательно, α1 = 3 – нижняя цена игры. Для определения верхней цены данной матрицы найдём максимальное значение элементов в столбцах матрицы Р1. По столбцам имеем (4, 5, 6, 5). Следовательно, β1 = 4. Поскольку α1 ≠ β1, то матрица Р1 не имеет седловой точки.
Аналогично, для матрицы P2 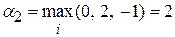 ,
,  . Таким образом, α1 = β2 = v = 2 – цена игры. Решение данной игры состоит в выборе игроком А стратегии А2, при этом его выигрыш не меньше 2; для игрока В оптимальной является стратегия В2, позволяющая ограничить его проигрыш этим же числом.
. Таким образом, α1 = β2 = v = 2 – цена игры. Решение данной игры состоит в выборе игроком А стратегии А2, при этом его выигрыш не меньше 2; для игрока В оптимальной является стратегия В2, позволяющая ограничить его проигрыш этим же числом.
а22 = 2 – седловая точка матрицы Р2. А2, В2 – чистые стратегии игроков А и В соответственно. Отклонение одним из игроков от оптимальной стратегии приводит к уменьшению выигрыша (для игрока А) и увеличению проигрыша (для игрока В).
Date: 2015-10-18; view: 897; Нарушение авторских прав