
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Стоимостная оптимизация сетевого графика при фиксированной величине критического пути
|
|
Рассмотрим случай, когда временные оценки для всех работ, включённых в сетевой график, установлены как минимально возможные и суммарная стоимость выполнения всего комплекса работ достигает максимума. Задача ставится следующим образом: при фиксированной продолжительности критического пути необходимо использовать резервы времени для некритических работ так, чтобы получить оптимальный вариант, сводящий к минимуму стоимость выполнения всего комплекса работ.
Пусть дан сетевой график, на котором для каждой из работ указаны минимально возможные оценки.
Зная коэффициенты изменения стоимости hij, можно для каждой работы определять стоимость её выполнения за время
tij(0) ≤ уij ≤ tij(1)
по формуле 
Так как находится оптимальный по стоимости вариант сетевого графика при заранее определённой продолжительности критического пути и известных критических работах, то сроки наступления критических событий известны и, следовательно, определены однозначно продолжительности критических работ.
С другой стороны, продолжительность некритических работ, имеющих резервы времени, может быть увеличена так, что каждая работа окажется на одном из критических путей.
Оптимальный вариант должен показать, в какой мере увеличиваются продолжительности некритических работ, при этом стоимость выполнения всего комплекса работ достигает минимума.
Поэтому в качестве неизвестных величин можно брать не продолжительность выполнения той или иной работы, а сроки наступления событий. Так как все события в оптимальном варианте становятся критическими, то срок наступления каждого из них однозначен (ранние и поздние сроки наступления критических событий совпадают). Тогда имеет место следующее соотношение:
уij = tj – ti,
где tj и ti – сроки наступления событий. Общая стоимость выполнения всего комплекса работ С выполняется как сумма стоимостей работ, т.е.

Составим систему ограничений модели.
Обозначим через К множество событий Рj, лежащих на критическом пути, а через R множество работ (i, j), не лежащих на критическом пути. Эти работы имеют резервы времени и их продолжительность может быть увеличена в пределах tij(0) ≤ уij ≤ tij(1).
Следовательно, разница между сроками наступления конечного и начального событий (tj – ti) для работ, принадлежащих R, может превышать величину tij(0). Отсюда система ограничений в математической модели оптимизации по стоимости сетевого графика задаётся условиями:
tj – ti ≥ tij(0), для любой работы (i, j)  R,
R,
tj = tj(0) = tj(1) для любых событий.
Окончательно математическая модель задачи оптимизации по стоимости сетевого графика имеет вид:

при условиях
tj – ti ≥ tij(0), (i, j)  R,
R,
tj = tj(0) = tj(1), Рj  К.
К.
Эта задача линейного программирования, и решается она симплексным методом.
Рассмотрим пример частичной оптимизации сетевого графика по стоимости при фиксированной величине критического пути в предположении, что стоимость всего комплекса работ можно уменьшить за счёт увеличения времени выполнения его некритических работ. Коэффициенты изменения стоимости определяются по формуле
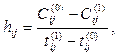
а уменьшение стоимости работы (i, j) – по формуле

где Cij(0) и Сij(1) – величины, в которых заключается стоимость работы (i, j) при её продолжительности в пределах tij(0) ≤ уij ≤ tij(1).
В дальнейшем будем предполагать, что величины hij уже рассчитаны и заданы, а продолжительность каждой работы целесообразно увеличить на величину такого резерва, чтобы не изменить ранние сроки наступления всех событий сети, т.е. на величину свободного резерва времени FSij.
Таким образом, если tij(1) – tij(0) > FSij, то в формуле для определения ∆Cij величина tij(1) – tij(0) заменяется на FSij.
Пусть задан некоторый комплекс работ, связывающий события и время выполнения работы (i j) – tij.
| Работа (i, j) | 1 – 2 | 1 – 3 | 1 – 5 | 2 – 3 | 2 – 4 | 2 – 6 | 3 – 5 | 3 – 6 | 3 – 8 | 3 – 11 |
| tij | ||||||||||
| Работа (i, j) | 4 – 7 | 4 – 9 | 5 – 8 | 6 – 9 | 7 – 10 | 8 – 11 | 9 – 12 | 10–13 | 11–12 | 12–13 |
| tij |
Окончательный вид сетевого графика с рассчитанными характеристиками:
– ранними и поздними (в скобках над событиями) сроками свершения событий;
– свободными резервами времени работ (в скобках рядом с продолжительностями работ) представлен на рисунке 6.8 (проверить самостоятельно):

Рисунок 6.8 – Сетевой график с рассчитанными характеристиками
Исходные данные для оптимизации и результаты оптимизации представлены в таблице 6.3.
Таблица 6.3 – Результаты частичной оптимизации сетевого графика
| Работа (i, j) | Продолжительность работы | Своб. резерв времени FSij | Стоимость работы Cij | Коэффициент изменения стоимости hij | tij(1) – tij(0) или FSij | Уменьше- ние стоимости ∆Cij | |
| tij(0) | tij(1) | ||||||
| (1, 2) (1, 3) (1, 5) (2, 3) (2, 4) (2, 6) (3, 5) (3, 6) (3, 8) (3, 11) (4, 7) (4, 9) (5, 8) (6, 9) (7, 10) (8, 11) (9, 12) (10, 13) (11, 12) (12, 13) | |||||||
| ИТОГО: | 1 152 |
Расчётная часть таблицы заполнена только для работ, имеющих свободный резерв времени, так как продолжительность только этих работ можно увеличить. В таблице подчёркнуты те работы, свободный резерв времени которых полностью исчерпан.
Стоимость первоначального варианта плана равна
 .
.
Стоимость нового плана равна
С – ∆С = 1 000,
т.е. уменьшилась на 13,2%.
Продолжительность критического пути равна 58. Новый план имеет вид:

Рассчитав временные характеристики полученного сетевого графика, получим, что он содержит пять критических путей (отмечены на графике удвоенными линиями).
Date: 2015-10-18; view: 885; Нарушение авторских прав