Коэффициента корреляции

Выборочный коэффициент корреляции, расчитанный по выборочным данным, есть точечной оценкой коэффициента корреляции, и в свою очередь, есть случайной величиной. Поэтому целесообразно сделать проверку гипотезы об отсутствии корреляционной связи. Для этого проверяется нулевая гипотеза

: (4)

и альтернативная гипотеза

: (5)

Предположим, что двухмерная случайная величина распределена по нормальному закону. Для выборки вычисляется t-статистика

(6)

которая имеет распределение Стьюдента с df= степенями свободы. Для заданной вероятности p и степеней свободы k находят табличное значение -статистики.

Если , то с заданной надежностью p гипотезу об отсутствии корреляционной связи между случайными величинами (X,Y) следует отвергнуть и принять альтернативную гипотезу о наличии зависимости между этими случайными величинами.

Величину называют выборочным коэффициентом детерминации. Для парной линейной регрессии коэффициент детерминации равен квадрату коэффициента корреляции. Используют также индекс корреляции (ρ) .

Надежные границы индекса корреляции определяются через оценки среднеквадратичного отклонения :

, . (7)

Стандартное отклонение углового коэффициента в и его доверительный интервал определяются по формуле , где

, (8)

- значение функции Стьюдента, которое определяется по заданным значениям вероятности и числом степеней свободы.

Стандартное отклонение свободного члена и его доверительный интервал определяются по формуле 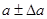, где

. (9)

Доверительный интервал регрессии определяется по формуле , где

(10)

Отметим, что наилучшие приближения с заданной надежностью следует ожидать в окрестности точки 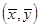. Надежная зона увеличивается при отдалении X от значения .

Date: 2015-10-22; view: 268; Нарушение авторских прав