Моделирование систем массового обслуживания с использованием метода Монте-Карло

В реальных условиях функционирования СМО име­ются переходные режимы, а входящие и исходящие потоки требо­ваний являются далеко не простейшими. В этих условиях для оцен­ки качества функционирования систем обслуживания широко ис­пользуют метод статистических испытаний (метод Монте-Карло). Основой решения задачи исследования функционирования СМО в реальных условиях является статистическое моделирование входя­щего потока требований и процесса их обслуживания (исходящего потока требований).

Для решения задачи статистического моделирования функциони­рования СМО должны быть заданы следующие исходные данные:

- описание СМО (тип, параметры, критерии эффективности рабо­ты системы);

- параметры закона распределения периодичности поступлений требований в систему;

- параметры закона распределения времени пребывания требова­ния в очереди (для СМО с ожиданием);

- параметры закона распределения времени обслуживания требо­ваний в системе.

Решение задачи статистического моделирования функционирова­ния СМО складывается из следующих этапов.

1. Вырабатывают равномерно распределенное случайное чис­ло .

2. Равномерно распределенные случайные числа преобразуют в величины с заданным законом распределения:

- интервал времени между поступлениями требований в систему ();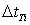

- время ухода заявки из очереди (для СМО с ограниченной дли­ной очереди);

- длительность времени обслуживания требования каналами ().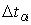

3. Определяют моменты наступления событий:

- поступление требования на обслуживание;

- уход требования из очереди;

- окончание обслуживания требования в каналах системы.

4. Моделируют функционирование СМО в целом и накаплива­ют статистические данные о процессе обслуживания.

5. Устанавливают новый момент поступления требования в си­стему, и вычислительная процедура повторяется в соответствии с изложенным.

6. Определяют показатели качества функционирования СМО путем обработки результатов моделирования методами математи­ческой статистики.

Методику решения задачи рассмотрим на примере моделирова­ния СМО с отказами.

Пусть система имеет два однотипных канала, работающих с от­казами, причем моменты времени окончания обслуживания на пер­вом канале обозначим через t _{1 i} , на втором канале - через t _{2 i} . Закон распределения интервала времени между смежными поступающи­ми требованиями задан плотностью распределения f ₁(t _T). Продол­жительность обслуживания также является случайной величиной с плотностью распределения f ₁(t _o).

Процедура решения задачи будет выглядеть следующим обра­зом:

1. Вырабатывают равномерно распределенное случайное чис­ло .

2. Равномерно распределенное случайное число преобразуют в величины с заданным законом распределения, используя формулы табл. 5.1. Определяют реализацию случайного интервала времени (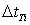) между поступлениями требований в систему.

3. Вычисляют момент поступления заявки на обслуживание: .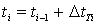

4. Сравнивают моменты окончания обслуживания предшеству­ющих заявок на первом t _{1(i -1)} и втором t _{2(i -1)} каналах.

5. Сравнивают момент поступления заявки t_i c минимальным моментом окончания обслуживания (допустим, что t _{1(i -1)} < _{2(i -1)}):

- если [ 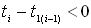] < 0, то заявка получает отказ и вырабатыва­ют новый момент поступления заявки описанным способом;

- если 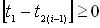, то происходит обслуживание.

6. При выполнении условия 5 б) определяют время обслужива­ния i -й заявки на первом канале 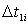путем преобразования случай­ной величины в величину (время обслуживания /-и заявки) с за­данным законом распределения.

7. Вычисляют момент окончания обслуживания i -й заявки на первом канале .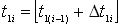

8. Устанавливают новый момент поступления заявки, и вычислительная процедура повторяется в соответствии с изложенным.

9. В ходе моделирования СМО накапливаются статистические данные о процессе обслуживания.

10. Определяют показатели качества функционирования системы путем обработки накопленных результатов моделирования методами математической статистики.

Date: 2015-10-21; view: 452; Нарушение авторских прав