Многоканальная модель с пуассоновским входным потоком и экспоненциальным распределением длительности обслуживания

В подавляющем большинстве случаев на практике системы мас­сового обслуживания являются многоканальными, и, следователь­но, модели с n обслуживающими каналами (где n > 1) представляют несомненный интерес.

Процесс массового обслуживания, описываемый данной моде­лью, характеризуется интенсивностью входного потока , при этом параллельно может обслуживаться не более n клиентов (заявок). Средняя продолжительность обслуживания одной заявки равняется . Входной и выходной потоки являются пуассоновскими. Режим функционирования того или иного обслуживающего канала не влияет на режим функционирования других обслуживающих каналов системы, причем длительность процедуры обслуживания каждым из каналов является случайной величиной, подчиненной экспоненциальному закону распределения. Конечная цель исполь­зования n параллельно включенных обслуживающих каналов за­ключается в повышении (по сравнению с одноканальной систе­мой) скорости обслуживания требований за счет обслуживания од­новременно n клиентов.

Граф состояний многоканальной системы массового обслужи­вания с отказами имеет вид, показанный на рис. 1.3.

Рис. 1.3. Граф состояний многоканальной СМО с отказами

Состояния СМО имеют следующую интерпретацию:

S ₀ - все каналы свободны;

S ₁ - занят один канал, остальные свободны;

…………………………………………………….

S_k - заняты ровно k каналов, остальные свободны;

…………………………………………………….

S_n - заняты все n каналов, остальные свободны;

Уравнения Колмогорова для вероятностей состояний системы P ₀ ,..., P_k,... P_n будет иметь следующий вид:

(1.26)

Начальные условия решения системы таковы:

P ₀(0) = 1, P ₁(0) = P ₂(0) =... = P_k (0) =... = P ₁(0) = 0.

Стационарное решение системы имеет вид:

(1.27)

где .

Формулы для вычисления вероятностей P_k называются формулами Эрланга.

Определим вероятностные характеристики функционирования многоканальной СМО с отказами в стационарном режиме:

 вероятность отказа:

_, (1.28)

так как заявка получает отказ, если приходит в момент, когда все n каналов заняты. Величина P_отк характеризует полноту обслуживания входящего потока;

 вероятность того, что заявка будет принята к обслуживанию (она же - относительная пропускная способность системы q) дополняет P_отк до единицы:

(1.29)

 абсолютная пропускная способность

(1.30)

 среднее число каналов, занятых обслуживанием (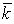) следующее:

(1.31)

Величина 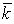характеризует степень загрузки СМО.

Пример 1.4. Пусть n -канальная СМО представляет собой вы­числительный центр (ВЦ) с тремя (n = 3) взаимозаменяемыми ПЭВМ для решения поступающих задач. Поток задач, поступаю­щих на ВЦ, имеет интенсивность = 1 задаче в час. Средняя про­должительность обслуживания = 1,8 час. Поток заявок на ре­шение задач и поток обслуживания этих заявок являются простей­шими.

Требуется вычислить финальные значения:

 вероятности состояний ВЦ;

 вероятности отказа в обслуживании заявки;

 относительной пропускной способности ВЦ;

 абсолютной пропускной способности ВЦ;

 среднего числа занятых ПЭВМ на ВЦ.

Определите, сколько дополнительно надо приобрести ПЭВМ, чтобы увеличить пропускную способность ВЦ в 2 раза.

Date: 2015-10-21; view: 489; Нарушение авторских прав