Решение. 1. Параметр потока обслуживании автомобилей:

1. Параметр потока обслуживании автомобилей:

2. Приведенная интенсивность потока автомобилей определя­ется как отношение интенсивностей и , т. е.

.

3. Вычислим финальные вероятности системы:

4. Вероятность отказа в обслуживании автомобиля:

.

5. Относительная пропускная способность поста диагностики:

.

6. Абсолютная пропускная способность поста диагностики

(автомобиля в час)

7. Среднее число автомобилей, находящихся на обслуживании и в очереди (т.е. в системе массового обслуживания):

8. Среднее время пребывания автомобиля в системе:

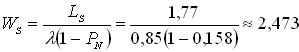часа

9. Средняя продолжительность пребывания заявки в очереди на обслуживание:

часа.

10. Среднее число заявок в очереди (длина очереди):

.

Работу рассмотренного поста диагностики можно считать удов­летворительной, так как пост диагностики не обслуживает автомо­били в среднем в 15,8% случаев (P_отк = 0,158).

Перейдем теперь к рассмотрению одноканальной СМО с ожиданием без ограничения на вместимость блока ожидания (т. е. ) Остальные условия функционирования СМО остаются без изменений.

Стационарный режим функционирования данной СМО существует при для любого n = 0, 1, 2,... и когда < . Система алгебраических уравнений, описывающих работу СМО при для любого n = 0, 1, 2,..._. имеет вид

. (1.20)

Решение данной системы уравнений имеет вид

, n = 0, 1, 2,... (1.21)

где .

Характеристики одноканальной СМО с ожиданием, без ограничения на длину очереди, следующие:

- среднее число находящихся в системе клиентов (заявок) на обслуживание:

(1.22)

- средняя продолжительность пребывания клиента в системе:

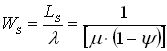(1.23)

- среднее число клиентов в очереди на обслуживании:

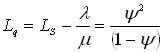(1.24)

- средняя продолжительность пребывания клиента в очереди:

(1.25)

Пример 1.3. Вспомним о ситуации, рассмотренной в примере 4.2, где речь идет о функционировании поста диагностики. Пусть рассматриваемый пост диагностики располагает неограниченным количеством площадок для стоянки прибывающих на обслуживание автомобилей, т. е. длина очереди не ограничена.

Требуется определить финальные значения следующих вероят­ностных характеристик:

- вероятности состояний системы (поста диагностики);

- среднее число автомобилей, находящихся в системе (на обслу­живании и в очереди);

- среднюю продолжительность пребывания автомобиля в системе (на обслуживании и в очереди);

- среднее число автомобилей в очереди на обслуживании;

- среднюю продолжительность пребывания автомобиля в очереди.

Date: 2015-10-21; view: 444; Нарушение авторских прав