
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Транспортная задача
|
|
Задание 4. Решить транспортную задачу.
Транспортная задача - это задача о перевозке некоторого груза от m поставщиков к n потребителям. Обычно условия транспортной задачи задаются в таблице.
| А\В |  
| 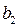
| 
| …… | 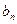
|

| 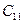
| 
| 
| …….. | 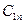
|

| 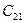
| 
| 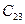
| ……. | 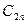
|
| …… | ……. | ……. | ……. | ……. | ……. |
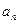
| 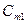
| 
| 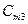
| ……. | 
|
В этой таблице:
 - запас груза у поставщика
- запас груза у поставщика 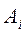 , где i=1, 2,…, m;
, где i=1, 2,…, m;
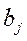 - потребность в грузе у потребителя
- потребность в грузе у потребителя  , где j=1, 2,…, n;
, где j=1, 2,…, n;
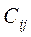 - стоимость перевозки единицы груза от i- го поставщика к j -му
- стоимость перевозки единицы груза от i- го поставщика к j -му
потребителю (тариф перевозки).
Если суммарный запас равен суммарным потребностям, т.е.  , то имеем закрытую модель транспортной задачи. Если нет, то открытую модель.
, то имеем закрытую модель транспортной задачи. Если нет, то открытую модель.
Рассмотрим решение закрытой модели транспортной задачи.
1. Как и при решении ЗЛП симплексным методом, определение оптимального плана транспортной задачи начинают с нахождения исходного опорного плана. Этот план наиболее рационально находить методом минимального элемента (существуют и другие методы его нахождения). Для этого в таблице тарифов выбираем минимальный (например 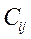 ) и в клетку, которая ему соответствует, помещаем наименьшее из чисел
) и в клетку, которая ему соответствует, помещаем наименьшее из чисел  и
и 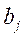 . Затем из рассмотрения исключаем либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены. Так на каждом шаге исключается либо один поставщик, либо один потребитель. При этом если клетка подлежит заполнению, но запасы равны нулю, то на этом шаге в соответствующую клетку заносится базисный нуль (0*). Из оставшейся части таблицы снова выбираем минимальный тариф и т.д. до тех пор, пока все запасы не будут распределены, а потребители удовлетворены. Если минимальных элементов несколько, то выбираем ту клетку, которой соответствует наибольшая перевозка. Таким образом, находим исходный опорный план. Этот опорный план должен содержать
. Затем из рассмотрения исключаем либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены. Так на каждом шаге исключается либо один поставщик, либо один потребитель. При этом если клетка подлежит заполнению, но запасы равны нулю, то на этом шаге в соответствующую клетку заносится базисный нуль (0*). Из оставшейся части таблицы снова выбираем минимальный тариф и т.д. до тех пор, пока все запасы не будут распределены, а потребители удовлетворены. Если минимальных элементов несколько, то выбираем ту клетку, которой соответствует наибольшая перевозка. Таким образом, находим исходный опорный план. Этот опорный план должен содержать 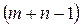 занятую клетку.
занятую клетку.
2. Для проверки найденного плана на оптимальность используется метод потенциалов.
2.1 Для «заняты х» клеток составляем систему уравнений
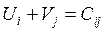 , где
, где 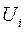 - потенциалы поставщиков,
- потенциалы поставщиков, 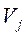 - потенциалы потребителей. Получаем
- потенциалы потребителей. Получаем 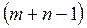 линейных уравнений с
линейных уравнений с  неизвестными. Такая система имеет множество решений. Чтобы найти любое из них, надо одной из переменных дать произвольное значение (например
неизвестными. Такая система имеет множество решений. Чтобы найти любое из них, надо одной из переменных дать произвольное значение (например  ). Находим значения остальных потенциалов.
). Находим значения остальных потенциалов.
2.2 Для «свободных» клеток находим числа  .
.
Если все 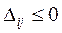 , то найденный опорный план будет оптимальным. Если есть хотя бы один
, то найденный опорный план будет оптимальным. Если есть хотя бы один  , то найденное решение не оптимально. Среди всех положительных
, то найденное решение не оптимально. Среди всех положительных 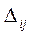 находим одно максимальное (например
находим одно максимальное (например  ) и делаем перераспределение поставок груза относительно свободной клетки
) и делаем перераспределение поставок груза относительно свободной клетки 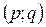 . Если среди всех положительных
. Если среди всех положительных  имеется несколько одинаковых максимальных, то выбираем любое.
имеется несколько одинаковых максимальных, то выбираем любое.
Перераспределение поставок в таблице условий транспортной задачи производится по циклу.
Цикл – это цепь, многоугольник, все вершины которого находятся в занятых клетках, углы прямые, число вершин четное. После того как цикл пересчета построен, в вершинах цикла, начиная со свободной клетки  , ставим поочередно «+» и «–». Далее в «–» клетках находим минимальный груз
, ставим поочередно «+» и «–». Далее в «–» клетках находим минимальный груз  , который прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Таким образом, свободная клетка
, который прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Таким образом, свободная клетка  становится занятой с грузом, а одна занятая клетка освобождается. Общее число занятых клеток в новом опорном плане должно сохраняться, т.е.
становится занятой с грузом, а одна занятая клетка освобождается. Общее число занятых клеток в новом опорном плане должно сохраняться, т.е. 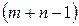 .
.
Этот новый план распределения поставок проверяем на оптимальность (переходим к пункту 2). Процесс продолжаем до тех пор, пока не получим, что все  . После того как оптимальный план перевозок будет найден, выписываем опорный план и находим минимальную стоимость перевозок.
. После того как оптимальный план перевозок будет найден, выписываем опорный план и находим минимальную стоимость перевозок.
Пример. Имеются четыре пункта поставки однородного груза  ,
, 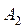 ,
, 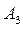 ,
, 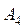 , в каждом из которых находится груз соответственно в количестве
, в каждом из которых находится груз соответственно в количестве 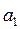 ,
, 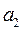 ,
,  ,
,  тонн и пять пунктов потребления этого груза
тонн и пять пунктов потребления этого груза 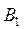 ,
, 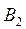 ,
, 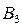 ,
, 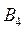 ,
,  . В пункты
. В пункты 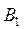 ,
, 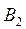 ,
,  ,
, 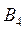 ,
,  требуется доставить соответственно
требуется доставить соответственно 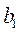 ,
, 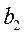 ,
, 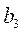 ,
,  ,
, 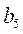 тонн груза. Транспортные расходы при перевозке единицы груза из пункта
тонн груза. Транспортные расходы при перевозке единицы груза из пункта 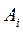 в пункт
в пункт 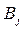 равны
равны 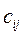 , где i= 1, 2, 3, 4, j= 1, 2, 3, 4, 5. Найти такой план закрепления потребителей за поставщиками, чтобы затраты по перевозкам были минимальными, при условии:
, где i= 1, 2, 3, 4, j= 1, 2, 3, 4, 5. Найти такой план закрепления потребителей за поставщиками, чтобы затраты по перевозкам были минимальными, при условии: 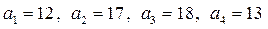 – пункты поставки груза,
– пункты поставки груза,
 – пункты потребления,
– пункты потребления,
 – тарифы.
– тарифы.
Решение. По условию задачи составим таблицу:
 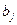
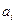
| 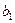
| 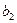
| 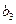
| 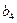
| 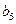
| |
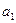
| ||||||

| ||||||
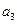
| ||||||

| ||||||
1. Найдем суммарный запас и суммарные потребности:
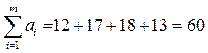 ,
,  .
.
Так как суммарный запас равен суммарным потребностям, т.е. 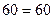 , то имеем закрытую модель транспортной задачи.
, то имеем закрытую модель транспортной задачи.
2. Находим исходный опорный план методом минимального элемента. Число занятых клеток должно равняться:  .
.
 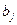
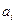
| 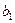
| 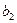
| 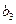
| 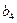
| 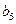
| |
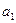
|   6 6
| 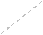 20 20
|  17 17
| 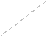 12 12
| ||

|    1 1
|  25 25
|    3 3
|  18 18
|   17 17
| |
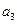
|     9 9
|
 5 5
|  18 18
| |||
 
| 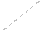  15 15
|  3 3
|  28 28
| |||
|  12 12
|
Среди всех тарифов перевозки 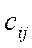 находим наименьший. В нашей задаче
находим наименьший. В нашей задаче  , в клетку
, в клетку 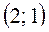 пишем наименьшее из чисел: запас поставщика
пишем наименьшее из чисел: запас поставщика 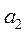 или потребности потребителя
или потребности потребителя 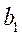 , т.е.
, т.е.  . Так как потребность первого потребителя
. Так как потребность первого потребителя 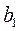 полностью удовлетворили, то его исключаем из дальнейшего рассмотрения, а запас у поставщика
полностью удовлетворили, то его исключаем из дальнейшего рассмотрения, а запас у поставщика 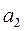 остался равным
остался равным 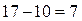 . Далее из оставшейся части таблицы снова выбираем наименьший тариф перевозки, и т.д. до тех пор, пока все запасы не будут распределены, потребители удовлетворены.
. Далее из оставшейся части таблицы снова выбираем наименьший тариф перевозки, и т.д. до тех пор, пока все запасы не будут распределены, потребители удовлетворены.
3. Проверяем найденный план на оптимальность методом потенциалов:
3.1 Для «занятых» клеток составляем уравнения 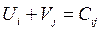 :
:

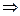
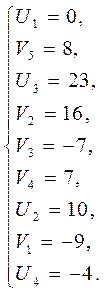
3.2 Для «свободных» клеток находим 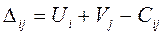 :
:
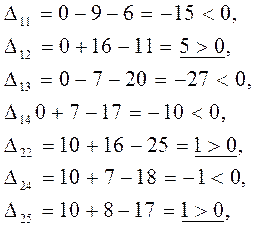
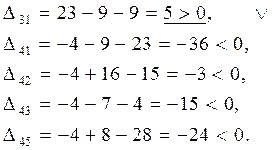
Строим в таблице цикл пересчета относительно клетки (3, 1). Он пойдет следующим образом (3, 1)  (2, 1)
(2, 1)  (2, 3)
(2, 3)  (3, 3).
(3, 3).
Расставляем знаки «+» и «–» в вершинах цикла, начиная с клетки (3, 1). В «–» клетках ищем минимальный груз  .Этот груз
.Этот груз 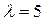 прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок:
прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок:
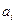
| 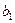
| 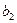
| 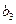
| 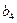
| 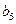
| |
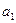
| ||||||

|    1 1
|    17 17
| ||||
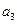
|  9 9
  5 5
|
 4 4
| ||||

| ||||||
4. Проверяем найденный план на оптимальность методом потенциалов.
4.1 Для «занятых» клеток:
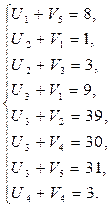
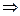

4.2 Для «свободных» клеток:
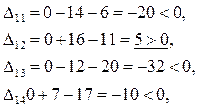


Строим в таблице цикл пересчета относительно клетки (2, 5). Он пойдет следующим образом (2, 5)  (2, 1)
(2, 1)  (3, 1)
(3, 1)  (3, 5).
(3, 5).
Расставляем знаки «+» и «–» в вершинах цикла, начиная с клетки (2, 5). В «–» клетках ищем минимальный груз 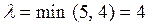 .Этот груз
.Этот груз 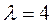 прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок:
прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок:
| 
| 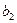
| 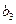
| 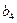
| 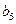
| |
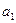
|     11 11
|   8 8
| ||||

|    1 1
|
  4 4
| ||||
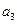
|  9 9
  9 9
|
 8 8
| ||||

| ||||||
5. Проверяем найденный план на оптимальность.
5.1 Для «занятых» клеток:
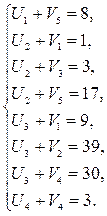
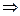
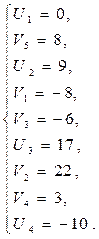
5.2 Для «свободных» клеток:
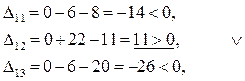
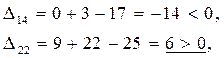
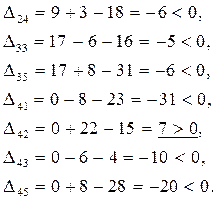
Строим в таблице цикл пересчета относительно клетки (1, 2). Он пойдет следующим образом (1, 2)  (1, 5)
(1, 5)  (2, 5)
(2, 5)  (2, 1)
(2, 1)  (3, 1)
(3, 1)  (3, 2).
(3, 2).
Расставляем знаки «+» и «–» в вершинах цикла, начиная с клетки (1, 2). В «–» клетках ищем минимальный груз 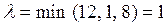 . Этот груз
. Этот груз 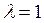 прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок:
прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок:
| 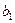
| 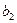
| 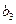
| 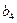
| 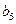
| |
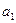
|    11 11
 1 1
|   8 8
| ||||

|  3 3
  12 12
|
  5 5
| ||||
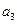
|
  7 7
|   16 16
| ||||

| ||||||
6. Проверяем найденный план на оптимальность.
6.1 Для «занятых» клеток:
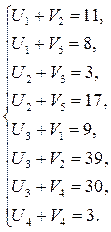
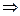
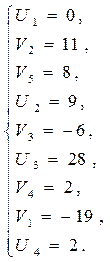
6.2 Для «свободных» клеток:
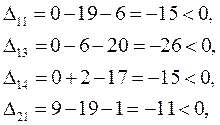

Строим в таблице цикл пересчета относительно клетки (3, 3). Он пойдет следующим образом (3, 3)  (2, 3)
(2, 3)  (2, 5)
(2, 5)  (1, 5)
(1, 5)  (1, 2)
(1, 2)  (3, 2).
(3, 2).
Расставляем знаки «+» и «–» в вершинах цикла, начиная с клетки (3, 3). В «–» клетках ищем минимальный груз 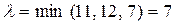 .Этот груз
.Этот груз  прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок:
прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок:
 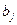
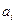
| 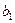
| 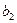
| 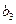
| 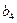
| 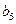
| |
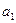
| ||||||

| ||||||
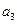
| ||||||

| ||||||
7. Проверяем найденный план на оптимальность.
7.1 Для «занятых» клеток:
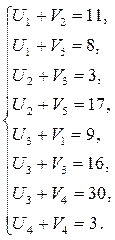
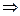

7.2 Для «свободных» клеток:



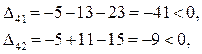
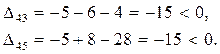
Так как все 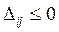 , найденный план является оптимальным.
, найденный план является оптимальным.
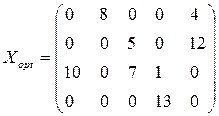
8. Найдем минимальную стоимость перевозок:
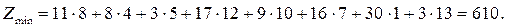
Ответ: 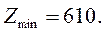
Date: 2015-10-18; view: 655; Нарушение авторских прав