Симплекс-метод решения задачи линейного программирования

Задание 3. Решить симплексным методом задачу линейного программирования (ЗЛП).

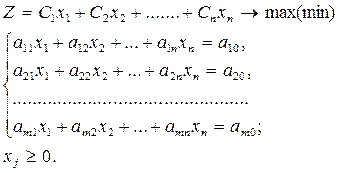
1. Прежде чем решать задачу симплексным методом, надо

проверить, что правые части системы ограничений неотрицательны, т.е. . Если это не так, то в соответствующем ограничении меняем знак.

2. Далее исходную задачу надо записать в канонической форме,

если она не имеет такой формы записи. Для этого каждое ограничение - неравенство вида «» надо превратить в равенство добавлением дополнительной неотрицательной (балансовой) переменной, а каждое ограничение - неравенство вида «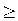» превратить в равенство вычитанием балансовой переменной. Таким образом, все ограничения в задаче будут уравнения с неотрицательными правыми частями.

3. Далее систему уравнений при помощи симплексных

преобразований надо привести к единичному базису, т.е. найти исходное опорное решение .

4. Для того чтобы проверить, будет ли это решение

оптимальным, надо составить оценочную строку (Z-строку) по следующему правилу: ,

где - искомый элемент Z-строки;

- столбец коэффициентов целевой функции при базисных переменных;

- столбец коэффициентов при неизвестном ;

- столбец свободных членов;

- скалярное произведение указанных столбцов – векторов;

- коэффициент целевой функции при неизвестном .

5. Для задачи на максимум.

Если в Z-строке все элементы положительные, , то найдено

оптимальное решение . Если же в Z-строке есть хотя бы один отрицательный элемент, то найденное решение не оптимально. Есть возможность его улучшения. Для этого среди отрицательных элементов Z-строки находим минимальный (например ). Столбец с номером p становится разрешающим. Разрешающую строку выбираем по симплексным преобразованиям (для этого в симплексной таблице заводится последний столбец). В столбце с номером p в качестве разрешающего элемента берется положительный элемент, если он один. Если в этом столбце положительных элементов несколько, то берется тот из них, для которого отношение свободных членов к этим положительным элементам будет наименьшее. Если в столбце с номером p вообще нет положительных элементов, то задача не имеет оптимального решения и . После того как разрешающий элемент найден, производим расчеты по методу Гаусса, включая и элементы Z-строки. Получаем новое опорное решение. После этого возвращаемся к началу пункта 5.

6. Для задачи на минимум. Если в Z-строке все элементы ,

то найдено оптимальное решение . Если же в Z- строке есть хотя бы один положительный элемент, то найденное решение не оптимально. Для улучшения решения среди положительных элементов Z-строки находим максимальный (например ). Столбец с номером q становится разрешающим. Разрешающую строку ищем по симплексным преобразованиям (смотреть задачу на максимум). Если в столбце с номером q нет положительных элементов, то задача не имеет оптимального решения и . После того, как разрешающий элемент выбран, выполняем расчеты по методу Гаусса, включая и элементы Z-строки, и получаем новое опорное решение. Переходим к началу пункта 6. Процесс продолжается до тех пор, пока не будет найдено оптимальное решение или мы не убедимся, что его нет.

Пример. Решить задачу линейного программирования симплексным методом

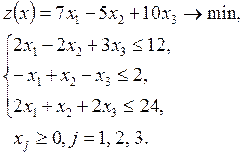
Решение. Приведем задачу к каноническому виду. Для этого в левую часть каждого неравенства типа «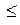» добавляем новые дополнительные переменные , , (новые балансовые переменные). Таким образом, задача примет вид

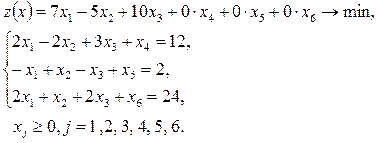
Составляем симплекс-таблицу.

	базис			-5
				-2					–
			-1	1	-1				2:1=2 – min
									24:1=24
			-7	5	-10
			-1		-1
							-1
		-10	-2		-5		-5

Так как есть исходное опорное решение, то составляем оценочную

Z-строку по следующему правилу: .

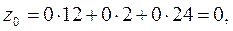
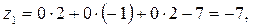
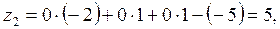
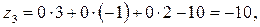
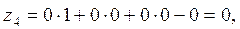
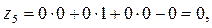
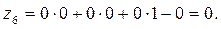
Так как среди есть одно положительное число, то столбик, в котором содержится этот элемент, выбираем в качестве разрешающего. Разрешающий элемент выбираем по методу минимального элемента (). Далее вычисления производим по методу Жордана–Гаусса.

Находим, что все , значит найденное решение оптимально, при этом , . Исходная задача имела три переменных, поэтому в ответе в оптимальном решении последние три дополнительные переменные не записываем.

Ответ: , .

Date: 2015-10-18; view: 423; Нарушение авторских прав