Задание 7. Решить транспортную задачу

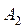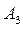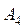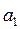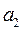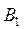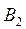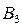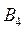Решить транспортную задачу. Имеются четыре пункта поставки однородного груза , , , , в каждом из которых находится груз соответственно в количестве , , , тонн и пять пунктов потребления этого груза , , , , . В пункты 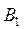, , 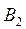, , 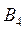требуется доставить соответственно 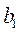, , 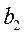, , 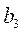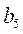тонн груза. Транспортные расходы при перевозке единицы груза из пункта 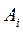в пункт 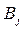равны 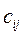, где i= 1, 2, 3, 4, j= 1, 2, 3, 4, 5. Найти такой план закрепления потребителей за поставщиками, чтобы затраты по перевозкам были минимальными, учитывая: ,

,

.

Вариант 4

Задание 1

Батарея из трех орудий производит залп по цели. Вероятности попадания в цель для каждого из них соответственно равны 0,7; 0,8 и 0,6. Найти вероятность того, что попадут в цель все три орудия.

Задание 2

Трое рабочих изготавливают однотипные изделия. Первый изготовил 40 изделий, 15 – второй и 25 – третий. Вероятности брака у каждого рабочего соответственно равны 0,05, 0,01, 0,02. Найти вероятность того, что наудачу взятая бракованная деталь изготовлена третьим рабочим.

Задание 3

Дано статистическое распределение выборки: в первой строке указаны выборочные варианты , а во второй строке – соответственные частоты количественного признака 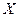. Требуется найти:

1) выборочную среднюю;

2) выборочное среднее квадратическое отклонение;

3) моду и медиану.

	12,4	16,4	20,4	24,4	28,4	32,4	36,4

Задание 4

Решить методом Жордана–Гаусса систему линейных уравнений:

Задание 5

Решить графически задачу линейного программирования:

Задание 6

Решить симплексным методом следующие задачи линейного программирования:

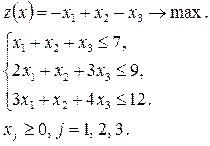
Задание 7

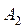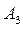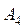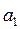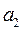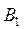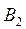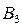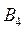Решить транспортную задачу. Имеются четыре пункта поставки однородного груза , , , , в каждом из которых находится груз соответственно в количестве , , , тонн и пять пунктов потребления этого груза , , , , . В пункты 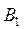, , 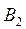, , 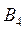требуется доставить соответственно 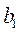, , 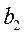, , 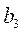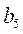тонн груза. Транспортные расходы при перевозке единицы груза из пункта 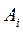в пункт 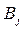равны 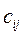, где i= 1, 2, 3, 4, j= 1, 2, 3, 4, 5. Найти такой план закрепления потребителей за поставщиками, чтобы затраты по перевозкам были минимальными, учитывая: ,

,

.

Вариант5

Задание 1

Вероятности землетрясения в каждом из трех городов соответственно равны 0,1; 0,8 и 0,6. Найти вероятность того, что землетрясение произойдет только в одном городе.

Задание 2

В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятности выполнить квалификационную норму соответственно равны 0,9, 0,8, 0,75. Найти вероятность того, что выбранный наудачу спортсмен выполнит норму.

Задание 3

Дано статистическое распределение выборки: в первой строке указаны выборочные варианты , а во второй строке – соответственные частоты количественного признака 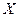. Требуется найти:

1) выборочную среднюю;

2) выборочное среднее квадратическое отклонение;

3) моду и медиану.

Задание 4

Решить методом Жордана–Гаусса систему линейных уравнений:

Задание 5

Решить графически задачу линейного программирования:

Date: 2015-10-18; view: 609; Нарушение авторских прав