
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Повторные испытания. Формула Бернулли
|
|
Если производится  независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события 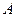 одна и та же и равна
одна и та же и равна 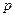 (
( ), то вероятность того, что событие
), то вероятность того, что событие 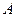 появится в этих
появится в этих  испытаниях ровно
испытаниях ровно  раз можно вычислить по формуле Бернулли:
раз можно вычислить по формуле Бернулли:
 , где
, где  .
.
Пример 19. Вероятность выиграть по лотерейному билету равна  . Найти вероятность выиграть по двум билетам из пяти.
. Найти вероятность выиграть по двум билетам из пяти.
Решение. По условию 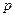 =
=  , значит
, значит  =
= 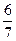 ;
;  = 5,
= 5,  = 2. Тогда по формуле Бернулли получаем
= 2. Тогда по формуле Бернулли получаем
P5(2) = 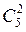

 =
=  = 0,1285.
= 0,1285.
Ответ: 0,1285.
Замечание: если число испытаний n велико, то применение формулы Бернулли приводит к громоздким вычислениям. В таких случаях пользуются предельными теоремами Лапласа.
Тема 2. Элементы математической статистики
Основные понятия и определения
Современная статистика разрабатывает планирование эксперимента, занимается последующим анализом и др. Если требуется изучить совокупность однородных объектов относительно некоторого признака, то на практике не изучают каждый элемент, а случайно отбирают ограниченное число объектов и изучают их.
Выборкой называют совокупность случайно отобранных объектов.
Генеральной называется совокупность объектов, из которых производится выборка.
Объем совокупности – это число объектов этой совокупности.
Наиболее удобно выборку записывать в виде таблицы:

| 
| … | 
|
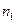
| 
| … | 
|
где наблюдаемые значения  называются вариантами (каждое из
называются вариантами (каждое из  наблюдалось
наблюдалось  раз), а указанная последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом,
раз), а указанная последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом, 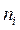 – частоты.
– частоты.
Выборочной средней  называется среднее арифметическое значение признака выборки
называется среднее арифметическое значение признака выборки
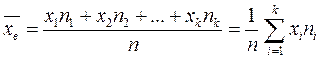 ,
,
где  – объем выборки.
– объем выборки.
Выборочной дисперсией  называется среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения
называется среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения  :
:
 ,
,
где  – объем выборки.
– объем выборки.
Выборочное среднее квадратическое отклонение  .
.
Исправленная дисперсия 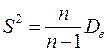 .
.
Исправленное среднее квадратическое отклонение  .
.
Аналогично теории вероятностей справедлива теорема о формуле для подсчета дисперсии.
Теорема: 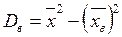 , где
, где  вычисляют по формуле:
вычисляют по формуле:
 .
.
Для упрощения счета числовых характеристик можно воспользоваться следующими формулами:
 ,
,  ,
,  ,
,  ,
,  , где с – варианта, имеющая максимальную частоту, h – шаг таблицы, т.е. интервал между соседними вариантами.
, где с – варианта, имеющая максимальную частоту, h – шаг таблицы, т.е. интервал между соседними вариантами.
Модой  называют варианту, которая имеет наибольшую частоту.
называют варианту, которая имеет наибольшую частоту.
Медианой 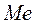 называют варианту, которая делит вариационный ряд на две части, равные по числу вариант.
называют варианту, которая делит вариационный ряд на две части, равные по числу вариант.
При этом если  , то
, то 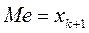 ,
,
если  , то
, то  .
.
Полигоном частот называют ломанную, отрезки которой соединяют точки  ,
, 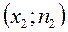 ,…,
,…, 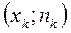 , где
, где  – варианты выборки,
– варианты выборки,  – соответствующие частоты.
– соответствующие частоты.
Пример 20. По данной выборке решить следующие подзадачи:
1. Получить статистическое распределение выборки;
2. Найти среднюю арифметическую 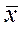 , дисперсию
, дисперсию  и среднеквадратичное отклонение
и среднеквадратичное отклонение  ;
;
3. Найти моду  и медиану
и медиану  .
.
Решение. Составим вариационный ряд:

| |||||||||

|
Объем выборки равен:  .
.
Найдем выборочную среднюю:
 .
.
Найдем выборочную дисперсию:
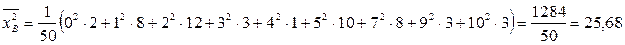
 .
.
Дисперсия  :
:  .
.
Среднеквадратичное отклонение  :
: 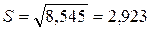 .
.
Мода: 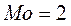 . Медиана:
. Медиана:  .
.
Date: 2015-10-18; view: 525; Нарушение авторских прав