
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Условная вероятность
|
|
Теорема 1 (сложения)
Если события 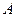 и
и  несовместны, то вероятность наступления хотя бы одного из событий равна сумме вероятностей этих событий, т.е.
несовместны, то вероятность наступления хотя бы одного из событий равна сумме вероятностей этих событий, т.е.
 .
.
Эта теорема обобщается на случай произвольного числа попарно несовместных событий:  .
.
Теорема 2 (сложения)
Вероятность наступления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления:  .
.
Событие 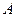 называется независимым от события
называется независимым от события  , если появление события
, если появление события 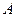 не зависит от появления события
не зависит от появления события  . В противном случае события называются зависимыми.
. В противном случае события называются зависимыми.
Условной вероятностью  называется вероятность события
называется вероятность события  , вычисленная в предположении, что событие
, вычисленная в предположении, что событие 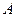 уже произошло.
уже произошло.
Теорема 3 (умножения)
Вероятность совместного появления двух событий 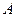 и
и  равна
равна

(причем неважно, которое из событий считать первым, а которое – вторым).
Если события 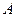 и
и  независимы, то теорема умножения примет вид:
независимы, то теорема умножения примет вид:
 .
.
Аналогично теорема умножения распространяется на случай нескольких событий:
для зависимых:  ,
,
для независимых:  .
.
Пример 13. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения первым равна 0,8, а вторым – 0,7.
Решение. Обозначим: А={поражение первым орудием}, В={поражение вторым орудием}. Тогда  = 0,8 × 0,7= 0,56 по теореме умножения для независимых событий.
= 0,8 × 0,7= 0,56 по теореме умножения для независимых событий.
Ответ: 0,56.
Пример 14. Два орудия произвели залп по цели. Вероятность поражения цели одним из них равна 0,8, а вторым – 0,7. Найти вероятность того, что цель была поражена только одним орудием.
Решение. По условию  = 0,8
= 0,8 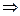
 = 0,2;
= 0,2;  = 0,7
= 0,7 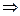
 = 0,3.
= 0,3.
Очевидно, что 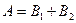 , где
, где 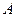 ={цель поражена только одним орудием},
={цель поражена только одним орудием},  ={цель поражена только первым},
={цель поражена только первым},  ={цель поражена только вторым}. По теореме сложения для несовместных событий
={цель поражена только вторым}. По теореме сложения для несовместных событий  . Причем
. Причем 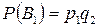 , a
, a  – по теореме умножения для независимых событий. Тогда
– по теореме умножения для независимых событий. Тогда  = 0,8 × 0,3 + 0,2 × 0,7 = 0,38.
= 0,8 × 0,3 + 0,2 × 0,7 = 0,38.
Ответ: 0,38.
Пример 15. Студент разыскивает формулу в трех справочниках. Вероятности того, что формула окажется в первом, втором, третьем справочниках соответственно равны 0,6, 0,7 и 0,8. Найти вероятности того, что формула окажется:
1) только в одном справочнике;
2) только в двух справочниках;
3) во всех трех справочниках.
Решение. По условию  ;
;
 ;
;
 .
.
1. Пусть 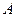 ={формула только в одном справочнике}, тогда
={формула только в одном справочнике}, тогда
 =0,6 × 0,3 × 0,2 + 0,4 × 0,7 × 0,2 + 0,4 × 0,3 × 0,8= = 0,188.
=0,6 × 0,3 × 0,2 + 0,4 × 0,7 × 0,2 + 0,4 × 0,3 × 0,8= = 0,188.
2. Пусть  ={формула только в двух справочниках}, тогда
={формула только в двух справочниках}, тогда  =0,6 × 0,7 × 0,2+0,4 × 0,7 × 0,8 + 0,6 × 0,3 × 0,8 = =0,452.
=0,6 × 0,7 × 0,2+0,4 × 0,7 × 0,8 + 0,6 × 0,3 × 0,8 = =0,452.
3. Пусть  ={формула во всех трех справочниках}, тогда
={формула во всех трех справочниках}, тогда
 = 0,6 × 0,7 × 0,8 = 0,336.
= 0,6 × 0,7 × 0,8 = 0,336.
Ответ: 1) 0,188; 2) 0,452; 3) 0,336.
Теорема 4 (вероятность появления хотя бы одного события).
Пусть известны вероятности появления каждого из  независимых событий:
независимых событий: 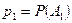 ,
, 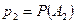 , …,
, …,  , тогда вероятность появления хотя бы одного из них равна
, тогда вероятность появления хотя бы одного из них равна  , где
, где  .
.
Пример 16. Студент разыскивает формулу в трех справочниках. Вероятности того, что формула окажется в первом, втором, третьем справочниках соответственно равны 0,6, 0,7 и 0,8. Найти вероятность того, что формула окажется хотя бы в одном справочнике.
Решение. По условию  ;
;
 ;
;
 .
.
Пусть 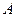 ={формула хотя бы в одном справочнике}, тогда
={формула хотя бы в одном справочнике}, тогда
 =1 – 0,4 × 0,3 × 0,2 = 0,976.
=1 – 0,4 × 0,3 × 0,2 = 0,976.
Ответ: 0,976.
Date: 2015-10-18; view: 1119; Нарушение авторских прав