Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Решение однородных систем линейных уравнений
|
|
Мы рассматривали задание подпространств в L в виде линейных оболочек систем векторов. Рассмотрим второй способ задания подпространств. Пусть е = {e1,…,еn} – базис пространства L, a 1 ,…,a п фиксированные элементы из P.
Утверждение. Подмножество
L1 = {x = x1e1+…+ xnеn Î L |a 1 x 1 +…+a n x n = 0} является
подпространством в L.
Доказательство. I. Пусть x = x1e1+…+ xnеn, у = у1e1+…+ + уnеn Î L1 Þ a1x1 +…+anxn = 0, a1у1 +…+anуn = 0 Þ
a1(x1+у1)+…+an(xп+уп)=0, a1ax1+…+anaxn=0 Þ х+у, axÎL1.
II. 2. Очевидно, 0L= 0e1+…+ 0еnÎ L1, так как a10 +…+an0= 0.
ÿ
Упражнение. Доказать, что не является подпространством в L подмножество {x= x1e1+…+xnеnÎL |a1x1+…+anxn=1}.
Пусть Li={x=x1e1+…+xnеnÎL|ai1x1+…+ainxn=0}, i =1,…,m. Тогда подпространство ∩Li задается однородной системой линейных уравнений
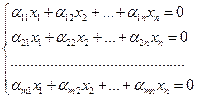. (7.1)
Это второй способ задания подпространств в L.
Пусть L= Pn. Тогда множество решений системы (7.1) является подпространством в P п. Найдем базис и размерность этого подпространства. С помощью элементарных преобразований приведем систему (7.1) к ступенчатому виду. Для простоты будем считать, что x1,…, xr – главные неизвестные, а xr+1,…, xт – свободные неизвестные, то есть матрица системы имеет следующий ступенчатый вид:
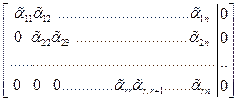. (7.2)
Будем придавать набору (п – r) свободных неизвестных значения (1,0,0,...,0,0), (0,1,0,…,0,0),…,(0,0,0,…,1,0), (0,0,0,…,0,1). После этого главные неизвестные находятся однозначно, и мы получим набор из (п – r) частных решений однородной
СЛУ f1 = (*,*,…,*,1,0,0,...,0,0), f2 = (*,*,…,*,0,1,0,...,0,0),…, fn-r= (*,*,…,*,0,0,...,0,0,1), где звездочкой * обозначены какие-то значения главных неизвестных. Покажем, что f1, f2 ,…,fn-r - базис в пространстве решений СЛУ (7.1). Во-первых, строки f1, f2,…,fn-r – линейно независимы. Это доказывается так же, как линейная независимость строк матрицы 
из 7.4. Во-вторых, любое решение СЛУ (7.1) является линейной комбинацией решений f1, f2 ,…, fn-r. В самом деле, если решение системы f = (с1,…,сr+1,..., сn), то линейная комбинация решений f0 = f - сr+1 f1 -... - сn fn-r принадлежит пространству решений, причем f0 = (*,…,*,0,…,0), то есть у f0 все свободные неизвестные равны нулю. Тогда, решая СЛУ (7.2), получим, что все главные неизвестные у f0 также равны нулю, то есть f0 = 0, f - сr+1 f1 -...- сn fn-r = 0 Þ f = сr+1 f1 +...+сn fn-r. Таким образом, f1, f2 ,…,fn-r - базис в пространстве решений СЛУ (7.1), и размерность пространства решений равна (п – r).
Определение. Базис в пространстве решений однородной системы линейных уравнений называется фундаментальной системой решений (сокращенно ФСР).
Так как базисы в пространствах выбираются неоднозначно, то и ФСР выбираются неоднозначно. Мы показали, что
f1, f2 ,…,fn-r – ФСР для СЛУ (7.1). Любое линейно независимое семейство из (п – r) решений также является фундаментальной системой решений.
Лекция 16.
Date: 2015-09-25; view: 357; Нарушение авторских прав