Результаты парных сравнений восьми сортов пива

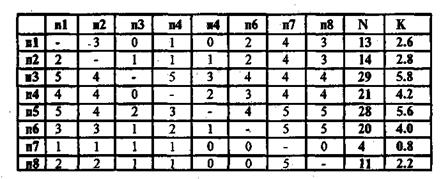
В двух последних столбцах соответственно приводятся общие показатели по всем респондентам: число предпочтений (N) и число предпочтений, приходящихся на одного респондента (К). Социо­лог обычно работает с относительными величинами типа К, а не с абсолютными типа N. В зависимости от значения К сорта пива по предпочтительности выстроились следующим образом:

пЗ > п5 > п4 > пб > п2 > п1 > п8 > п7

Если социолога интересует только ранжированный ряд сортов пива, то можно считать задачу решенной. Столь трудоемкая проце­дура парных сравнений была бы неэффективной, если бы в резуль­тате ее применения не получались и другие важные выводы. Значе­ния К имеют количественный характер, они получены по метрической шкале. Поместив сорта пива на линеечку в зависимо­сти от значения К (от 0,8 до 5.8), имеем следующую картину:

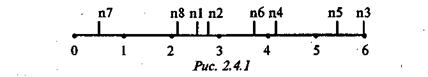
Из рис. 2.4.1 видно, во сколько и насколько один сорт предпоч­тительнее другого. Сорта п1 (К=2,6) и п2 (К=2,8) практически нераз­личимы. Аналогична ситуация для п6 и п4, а также для п5 и п3. Резко выделяются четыре типологические группы, к которым, по-видимо­му, принципиально разное отношение респондентов. В первую груп­пу входит «Жигулевское» (п7), во вторую ¾ «Очаковское» (п8), «Bavaria» (nl) и «White Bear» (п2), в третью ¾ «Tuborg» (п6), «Афанасий» (п4), в четвертую ¾ «Балтика» (п5) и «Gueness» (пЗ). Опять же характер рас­пределения показателя К диктует логику дальнейшего анализа, если социолога интересует не только ранжирование.

Отметим интересный факт: на входе изначально мы имели номинальный уровень измерения, а на выходе имеем метрическую шкалу. Более трудоемкие приемы измерения, такие, как метод равнокажущихся интервалов и метод парных сравнений, приводят нас к количественным оценкам, к метрическому уровню измерения в нашем понимании. Напомним, что мы исходим в книге из грубого деления всех шкал на три типа: номинальные, порядковые и метри­ческие. На самом деле в упомянутых двух методах все обстоит зна­чительно сложнее и получаются не совсем метрические шкалы. Но этот сюжет уже для следующего уровня вашего познания социоло­гии. Мои попытки введения других типов шкал для начального обу­чения методологии не увенчались успехом. Поэтому для нас с вами метрические шкалы ¾ это те, когда уровень измерения выше поряд­кового, и то, что похоже на числа, на количества.

Однако следует особо оговорить тот факт, что в результате использования метода парных сравнений получается метрическая шкала. Это доказано Терстоуном, исходя из того, что в динамике предпочте­ния отдельного респондента характерен нормальный закон распреде­ления. Что это значит? Если спрашивать респондента много раз, то каждый раз он будет давать различные оценки (по предпочтению). Это естественно. Но его оценки будут подчиняться нормальному за­кону распределения, т. е. отклонения от некоторой средней оценки будут носить случайный характер.

Прежде, чем перейти к сравнительному анализу двух рассмот­ренных методов ранжирования, остановимся на условии примени­мости метода парных сравнений.

Date: 2015-09-24; view: 372; Нарушение авторских прав