Тертя кочення

Тертям кочення називають опір, що виникає при коченні одного тіла по поверхні іншого тіла.

В реальних умовах поверхня тіла, що котиться, і площина, по якій тіло котиться, не абсолютно тверді, а дещо деформуються внаслідок тиску тіла на площину.

Кочення викликано деформацією тіл і рух відбувається під дією двох пар сил (, ) і (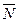, 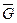), які показано на рисунку 30.

Рисунок 30

Момент пари (, ) - 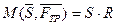викликає кочення тіла і називається моментом кочення (обертання) 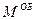. Його плечем є радіус котка (рисунок 30).

Момент пари (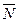, 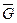) - 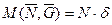чинить опір повороту тіла і називається моментом опору кочення 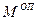(рисунок 30). У момент початку руху

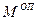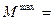
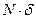= , (30)

де 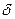(плече пари) – коефіцієнт тертя кочення.

Одиниці вимірювання 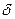- це одиниці довжини, найчастіше сантиметри (см).

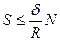- умова кочення котка.

Умова кочення без ковзання .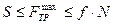

7.3 Тертя вертіння

Опір вертіння виникає внаслідок тертя кулі по площині. (Приклад – упорний підшипник подп’ятнік).

. (31)

де - сила нормального тиску кулі на площину, яка в даному випадку дорівнює значенню ваги тіла;

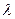- коефіцієнт тертя вертіння, має розмірність довжини (метр, сантиметр), малий за величиною (у 5 – 10 разів меньший за коефіцієнт тертя кочення < ).

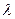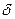8 Довільна просторова система сил

8.1 Момент сили відносно осі

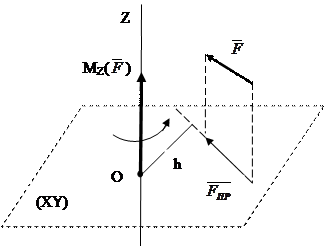
Момент сили відносно осі – це алгебраїчна величина (число), яка дорівнює моменту проекції цієї сили на площину, перпендикулярну осі, відносно точки перетину осі з площиною (рисунок 31).

(32)

Рисунок.31

Момент буде вважатись додатнім, якщо з кінця осі Z поворот, який сила намагається створити, можна побачити спрямованим проти стрілки годинника, і від’ємним, якщо за стрілкою годинника.

Момент сили відносно осі буде дорівнювати нулю, якщо сила і вісь лежать в одній площині, тобто:

1) сила паралельна осі, тому що при цьому =0;

2) лінія дії сили перетинає вісь, тому що при цьому 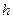=0.

Аналітичні визначення моментів сили відносно осей координат.

,

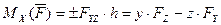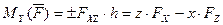, (33)

.

Момент сили відносно центра (точки) в просторі прикладається в центрі О (рисунок 32) та за модулем визначається за рівнянням:

. (34)

Рисунок 32

Залежність моментів сили відносно точки і осі, яка проходить через цю точку (центр):

Момент сили відносно осі дорівнює проекції на цю вісь вектора, утворюючого момент даної сили відносно будь – якого центра, що проходить через цю вісь (рисунок 33)

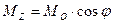(35)

- момент сили відносно осі Z;

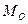- момент сили відносно центру О.

Рисунок 33

8.2 Визначення головного вектора та головного момента просторової системи сил

Головним вектором системи 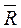називається вектор, прикладений у центрі приведення, що дорівнює геометричній сумі всіх сил системи:

= . (36)

Головний момент системи 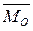відносно даного центра дорівнює геометричній сумі моментів всіх сил відносно центра О

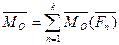. (37)

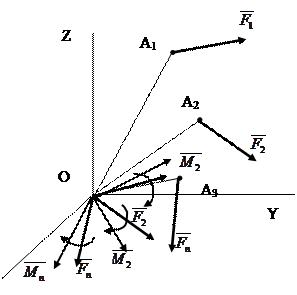Рисунок 34

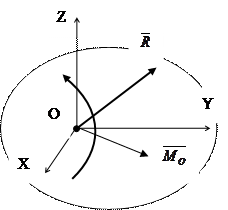За основною теоремою статики, будь – яка система сил, діючих на абсолютно тверде тіло, при приведенні до довільно обраного центра О може бути замінена одною силою , що дорівнює головному вектору системи і прикладається в центрі приведення О, та одною парою з моментом , що дорівнює головному моменту системи відносно центра приведення О (рисунок 35).

Рисунок 35

Аналітичне визначення векторів та

1 Проекції головного вектора системи на координатні осі:

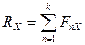, , . (38)

Модуль головного вектора: 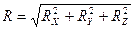. (39)

Напрямок головного вектора

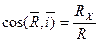, , . (40)

2 Проекції головного моменту системи

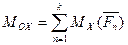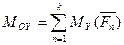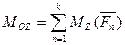, , . (41)

Модуль головного моменту 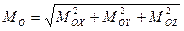. (42)

Напрямок головного моменту системи

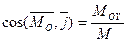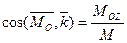, , . (43)

Системи сил, для яких та співпадають, статично еквівалентні.

Випадки приведення просторової системи сил

1 та - система знаходиться в стані рівноваги.

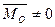2 та - система приводиться до пари сил, момент якої дорівнює головному моменту системи. Вільне тіло під дією такої системи може рухатись обертально.

3 , - система сил приводиться до рівнодійної, лінія дії якої проходить через центр приведення. Вільне тіло під дією такої системи може рухатись поступально (якщо рівнодійна проходить через центр ваги тіла).

4 , , 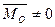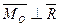( =0) - система приводиться до рівнодійної, лінія дії якої не проходить через центр приведення (рисунок 36).

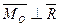- нормальний головний момент

(перпендикулярний) головному

вектору системи (),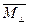

Рисунок 36 - найменший головний момент.

5 , , 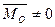, 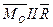() - система приводиться до динамічного гвинта (динами сил) – сукупності сили та пари, що розташована у площині, перпендикулярній силі (рисунок 37).

Вісь динами - лінія дії сили , яка проходить через центр приведення (рисунок 37).

Найменший головний момент визначається

за формулою:

Рисунок 37 .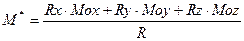

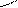
6 , , , ,

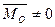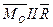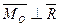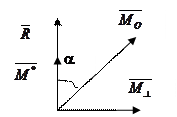- система приводиться до динами сил, вісь якої не проходить через центр приведення О (рисунок 38).

Рисунок 38

8.3 Аналітичні умови рівноваги довільної просторової системи сил

Для рівноваги довільної просторової системи сил необхідно і достатньо, щоб суми проекцій всіх сил на кожну з трьох координатних осей і суми їх моментів відносно цих осей дорівнювали нулю.

, , ,

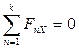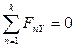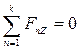(44)

, , .

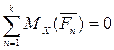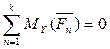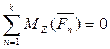Date: 2015-09-24; view: 415; Нарушение авторских прав