Головний вектор та головний момент системи сил

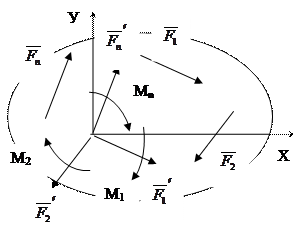
Рисунок 22

Головним вектором системи 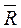називається вектор, що дорівнює геометричній сумі всіх сил системи.

= . (17)

Модуль :

, , .

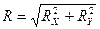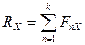Напрямок вектора :

, .

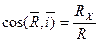Головним моментом системи 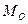відносно центра Ов площиніназивається алгебраїчна сума моментів сил системи відносно центра приведення О.

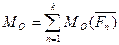. (18)

Головний вектор не залежить від обирання центра приведення О.

Головний момент сил 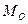залежить від центра приведення.

Головний вектор і головний момент 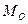називають елементами приведення системи.

Для завдання системи сил достатньо завдати її головний вектор і головний момент відносно центра приведення 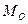(рисунок 23).

Рисунок 23

Основна теорема статики про приведення системи сил до даного центра:

Будь – яка плоска довільна система сил, діючих на абсолютно тверде тіло, при приведенні до довільно обраного центра О, може бути замінена одною силою , що дорівнює головному вектору системи і прикладається в центрі приведення О, та одною парою з моментом 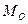, що дорівнює головному моменту системи відносно центра О.

Випадки приведення плоскої системи сил до простішого вигляду

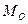1 = 0 і = 0 - система знаходиться в стані рівноваги.

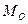
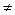2 = 0 і 0 – система приводиться до пари з моментом, який дорівнює головному моменту системи 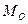. Система може викликати обертальний рух тіла, до якого прикладена.

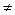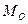3 0 і = 0 – система приводиться до рівнодійної , яка проходить через центр О. Під дією такої сили тіло, на яке вона діє, може рухатись поступально в напрямку вектора сили .

4 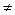0, 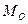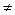0 – система приводиться до рівнодійної , яка прикладається в іншій точці, що не проходить через центр О.

4.2 Умови рівноваги довільної плоскої системи сил

1 Геометричні умови рівноваги:

для рівноваги плоскої довільної системи сил необхідно і достатньо, щоб водночас головний вектор і головний момент системи дорівнювали нулю:

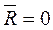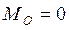, . (19)

2 Аналітичні умови рівноваги

Основна форма умов рівноваги

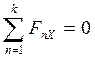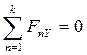, , . (20)

Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми проекцій всіх сил на координатні вісі та сума їх моментів відносно будь – якого центра, який лежить у площині дії сил, дорівнювали нулю.

Друга форма умов рівноваги

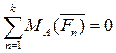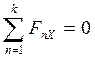, , . (21)

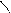Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми моментів всіх сил відносно будь – яких двох центрів А і В та сума їх проекцій на вісь ОХ, не перпендикулярну до прямій АВ 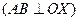, дорівнювали нулю.

Третя форма умов рівноваги (рівняння трьох моментів)

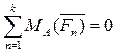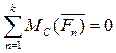, , . (22)

Для рівноваги плоскої довільної системи сил необхідно і достатньо, щоб суми моментів всіх сил відносно будь – яких трьох центрів А, В і С, що не лежать на одній прямій, дорівнювали нулю.

Рівновага плоскої системи паралельних сил

Система сил { 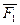, ,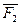.. } (рисунок 24) паралельних осі ОУ.

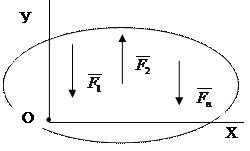1 форма:

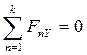, (23)

2 форма:

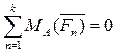, (24)

Рисунок 24 точки А і В не повинні належати прямій,

паралельній силам.

Date: 2015-09-24; view: 4711; Нарушение авторских прав