Побудова векторного силового багатокутника

Послідовно паралельним перенесенням кожного вектора сили в кінцеву точку попереднього вектора складається багатокутник, сторонами якого є вектори сил системи, а замикаючою стороною – вектор рівнодійної системи збіжних сил (рисунок 11).

Рисунок 11

2.2 Умови рівноваги системи збіжних сил

Геометрична умова рівноваги збіжної системи сил:

для рівноваги системи збіжних сил необхідно і достатньо, щоб векторний силовий багатокутник, побудований на цих силах, був замкнутим.

=0. (4)

Аналітичні умови рівноваги системи збіжних сил:

для рівноваги системи збіжних сил необхідно і достатньо, щоб алгебраїчні суми проекцій всіх сил на координатні вісі дорівнювали нулю.

= 0, = 0, 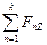= 0. (5)

Рівняння (5) є умовою рівноваги системи збіжних сил, розташованих у просторі.

2.3 Момент сили відносно центра

Будь – який кінематичний стан тіл, які мають точку або вісь обертання, можна описати моментом сили, котрий характеризує обертальний ефект дії сили.

Момент сили відносно центру як вектор - це векторний добуток радіус – вектора 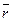точки прикладання сили на вектор сили .

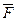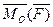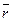
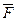= (6)

Сила 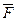прикладена до точки А, радіус–вектор якої відносно довільного центра О визначається, як 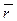= 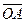(рисунок 12).

Рисунок 12.

Модуль моментусили визначається за векторним добутком 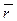і 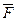та кутом α між радіус – вектором та вектором сили:

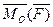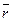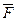| | = | | · | |·sin ( 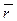^ 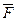) = | |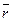· | |·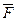sin (α) = r·F· sin α = F· h. (7)

Величина (r·sin α) = h – називається плечем сили – найкоротша відстань від центра (точки) до лінії дії сили (перпендикуляр із центра на лінію дії сили) (рисунок 12).

Вектор 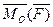спрямовується за правилом векторного добутку: момент сили відносно центра (точки) як вектор, спрямовується перпендикулярно площині, в якій розміщені сила і центр так, щоб з його кінця було видно намагання сили повертати тіло навколо центра проти ходу стрілки годинника.

Алгебраїчна величина моменту сили

Момент сили відносно центра в площині – алгебраїчна величина, яка дорівнює добутку модуля сили 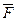на плече 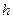відносно того ж центра з урахуванням знака.

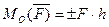. (8)

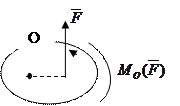
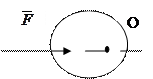
Знак моменту сили залежить від напрямку, в якому сила намагається обертати центр (рисунок 13):

1) проти ходу стрілки годинника – 2) за стрілкою годинника –

„+” (додатній); „-” (від’ємний).

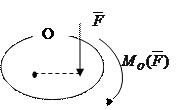Рисунок 13

Одиницею вимірювання моменту сили є 1 ньютон на метр (Hм).

Властивості моменту сили відносно центра (точки)

1 Модуль моменту сили відносно точки дорівнює подвоєній площі трикутника, побудованого на векторах 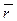і .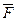

= АВ · h = 2 S_∆ОАВ, (9)

де S_∆ОАВ = АВ· h ∕ 2 (рисунок 12).

2 Момент сили відносно точки не змінюється при перенесенні сили вздовж її лінії дії, оскільки незмінним залишається плече сили.

3 Момент сили відносно центра (точки) дорівнює нулю , коли:

- сила дорівнює нулю F = 0;

Рисунок 14 - плече сили h = 0, тобто лінія дії сили проходить

через центр (рисунок 14).

Теорема Варіньона (про момент рівнодійної)

;

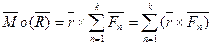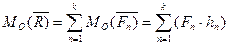(10)

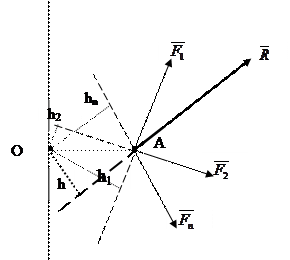
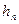- плечі сил системи відносно центра О.

Рисунок 15

Теорема:

Момент рівнодійної плоскої системи збіжних сил відносно будь - якого центра дорівнює алгебраїчній сумі моментів складових сил системи відносно того ж центра (рисунок 15)

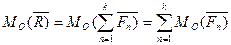. (11)

3 Теорія пар сил

Date: 2015-09-24; view: 1227; Нарушение авторских прав