Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Тема 1. Эквивалентность множеств
|
|
1. Взаимно однозначное соответствие.
2. Эквивалентные множества.
3. Понятие мощности множества.
См. список литературы: [4, гл. 1.6]; [5, гл.1.3].
Краткие теоретические сведения
Отображение f: А → В называется взаимно однозначным соответствием, если для любого y 
В найдется один элемент х А такой, что f(x) = y.
Если между множествами А и В можно установить взаимно однозначное соответствие, то множества называются эквивалентными или равномощными. Это обозначается так: А ~ В.
Задачи
1. Привести примеры элементарных функций, устанавливающих взаимно однозначное соответствие между областью определения и множеством значений.
2. Установить взаимно однозначное соответствие между:
а) отрезками [ a; b ] и [ c; d ];
б) интервалами (a; b) и (c; d);
в) полуинтервалом [0; 1) и лучом [0; ∞).
3. Устанавливают ли функци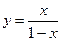и 
и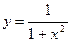 
взаимно однозначное соответствие между областью определения и множеством значений?
4. Пусть φ: А → В – строго монотонная функция. Доказать, что отображение φ – взаимно однозначное.
5. Пусть φ: (a; b) → (c; d) – непрерывная функция, имеющая экстремум в точке х0 (a; b). Показать, что отображение φ не является взаимно однозначным.
6. Можно ли с помощью непрерывной функции взаимно однозначно отобразить
а) отрезок [ a; b ] на интервал (a; b);
б) отрезок [ a; b ] на множество [ c; d ] 
[ m; n ], где [ c; d ]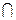 
[ m; n ] = Ø? 
7. Показать, что отношение эквивалентности (~) обладает следующими свойствами:
a) А ~ А – рефлексивность;
b) (А ~ В)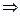 
(В ~ А) – симметричность;
c) (А ~ В)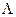 
(В ~ С) 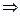(А ~ С) – транзитивность.
8. Показать, что если А ~ А1, В ~ В1 и А 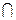В = Ø, А1 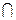В1 = Ø,
то А В ~ А1 В1.
9. Пусть А = 
А i, B = B i и А i 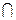A j = Bi 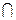Bj при i 
j. Доказать, что если А i ~ B i, то А ~ В.
10. Пусть f: X → Y – взаимно однозначное отображение; А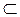 
X, B 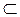Y. Доказать: f (А 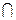В) = f (А) 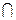f (В).
11. Пусть f: X → Y – взаимно однозначное отображение; А 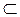X, B 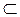Y. Доказать: f (А \ В) = f (А) \ f (В).
12. Пусть А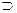 
В 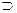С и φ: A → C – взаимно однозначное отображение. Показать, что А \ В ~ С \ φ(В).
13. Установить взаимно однозначное соответствие между отрезком [0;1] и интервалом (0; 1).
14. Используя результаты задачи №13, установить взаимно однозначное соответствие между
а) отрезком [0; 1] и числовой прямой (– ∞; ∞);
б) лучом [0; ∞) и интервалом (a; b).
15. Покажите, что любые два из бесконечных множеств действительных чисел: [α; β], [α; β), (α; β], (α; β), [α; ∞), (α; ∞), (– ∞; β], (– ∞; β) и (– ∞; ∞), где α, β – действительные числа и α < β, являются равномощными.
16. Установить взаимно однозначное соответствие между множеством всех рациональных чисел отрезка [0;1] и множеством всех точек с рациональными координатами квадрата [0;1]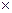 
[0;1].
17. Докажите равномощность множества действительных и множества иррациональных чисел.
Date: 2015-09-24; view: 1333; Нарушение авторских прав