
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задание 5 (дополнительное). Определение сил реакций составной конструкции с помощью
|
|
принципа возможных перемещений (ПВП)
Для конструкции, приведенной в задании 1, определить силы реакции и внутренние силы взаимодействия сочлененных тел с помощью методов аналитической механики.
Указания. Задание 5 – на применение принципа Лагранжа (принципа возможных перемещений) для решения задач статики (см. приложение И). При его решении надо рассмотреть равновесие каждого из тел системы, изобразив их отдельно и приложив к ним все внешние силы и силы реакции, действующие на данную часть системы. При этом внутренние силы взаимодействия тел превратятся во внешние для каждого отдельного тела. Система имеет одну степень свободы и у неё одно независимое возможное перемещение. Для составления уравнения необходимо сообщить системе возможное (малое) перемещение и составить уравнение работ всех активных сил на этом перемещении. Дальнейший ход решения задачи разъяснен в примере 6.
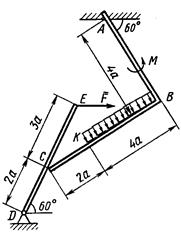 Пример 6
Пример 6
На угольник  (
(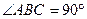 ), конец
), конец 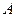 которого жестко заделан, в точке
которого жестко заделан, в точке 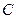 опирается стержень
опирается стержень 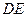 (рис. 5.0, а). Стержень имеет в точке
(рис. 5.0, а). Стержень имеет в точке 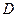 неподвижную шарнирную опору и к нему приложена сила
неподвижную шарнирную опору и к нему приложена сила 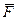 , а к угольнику – равномерно распределенная на участке
, а к угольнику – равномерно распределенная на участке 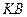 нагрузка интенсивности
нагрузка интенсивности 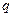 и пара с моментом
и пара с моментом 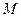 .
.
 Дано:
Дано: 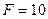 кН,
кН, 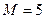
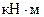 ,
, 
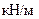 ,
,  м.
м.
Определить: реакции в точках 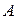 ,
, 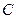 ,
, 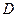 .
.
Решение:
Рассмотрим способ решения примера 1 с помощью ПВП. Разобьем систему на части в точке 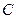 соединения стержня и угольника.
соединения стержня и угольника.
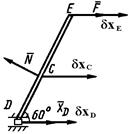
1) Рассмотрим равновесие стержня (рис. 5.0, а).
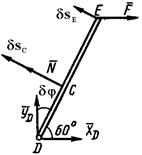 Равномерно распределенную нагрузку заменяем силой
Равномерно распределенную нагрузку заменяем силой 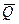 , приложенной в середине участка
, приложенной в середине участка 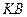 (
( кН).
кН).
 Для применения ПВП отбросим внутреннюю одностороннюю связь в точке
Для применения ПВП отбросим внутреннюю одностороннюю связь в точке 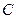 , заменив ее действие силой
, заменив ее действие силой 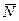 , направленной перпендикулярно к стержню. В результате, полученная система приобрела одну степень свободы: возможным перемещением части
, направленной перпендикулярно к стержню. В результате, полученная система приобрела одну степень свободы: возможным перемещением части 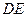 является ее поворот вокруг неподвижного шарнира
является ее поворот вокруг неподвижного шарнира 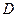 на угол
на угол 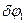 .
.
 Составим уравнение работ, выражающее ПВП. При этом учтем, что работа силы при повороте тела равна произведению момента силы относительно центра вращения на угол поворота тела:
Составим уравнение работ, выражающее ПВП. При этом учтем, что работа силы при повороте тела равна произведению момента силы относительно центра вращения на угол поворота тела:
 . (1)
. (1)
Выразим связь между возможными перемещениями точек 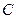 и
и 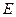 и углом поворота стержня:
и углом поворота стержня:
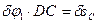 ,
, 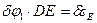 .
.
Подставляем все величины в уравнение для работы (1):
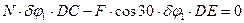
Сокращаем его на 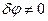 и находим
и находим
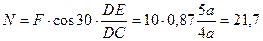 кН.
кН.
Чтобы найти реакцию 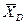 , заменим неподвижную опору в точке
, заменим неподвижную опору в точке 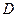 ползуном с горизонтальной направляющей и, считая движение стержня поступательным, придадим ему возможное перемещение (рис. 5.0, б).
ползуном с горизонтальной направляющей и, считая движение стержня поступательным, придадим ему возможное перемещение (рис. 5.0, б).
 При этом
При этом
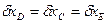 .
.
Применяем ПВП:
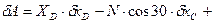 .
. 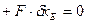 (2)
(2)
Вычисляем:
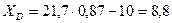 кН.
кН.
 Аналогично, чтобы найти реакцию
Аналогично, чтобы найти реакцию 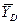 , заменим неподвижную опору в точке
, заменим неподвижную опору в точке 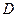 ползуном с вертикальной направляющей и, считая движение стержня поступательным, придадим ему возможное перемещение (рис. 5.0, в).
ползуном с вертикальной направляющей и, считая движение стержня поступательным, придадим ему возможное перемещение (рис. 5.0, в).
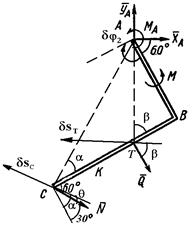
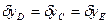 ,
,

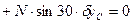 , (3)
, (3)
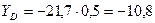 кН.
кН.
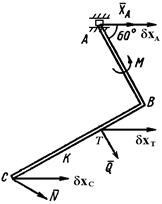
2) Рассмотрим равновесие угольника (рис. 5.0, г).
 Так как в точке
Так как в точке 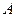 – заделка, то угольник может лишь вращаться вокруг этой точки в плоскости рисунка. Таким образом, точка
– заделка, то угольник может лишь вращаться вокруг этой точки в плоскости рисунка. Таким образом, точка 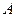 для угольника является мгновенным центром скоростей. Придадим угольнику возможное перемещение
для угольника является мгновенным центром скоростей. Придадим угольнику возможное перемещение 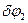 и выразим через него возможные перемещения точек
и выразим через него возможные перемещения точек 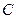 и
и  , используя свойства МЦС:
, используя свойства МЦС:
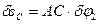 ,
, 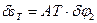 .
.
Применяем ПВП:
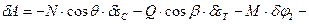
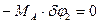 . (4)
. (4)
Учитывая, что геометрически
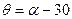 ,
,
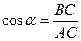 ,
,
 ,
,
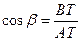 ,
,
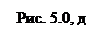
 ,
,
из (4) находим:
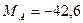
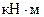 .
.
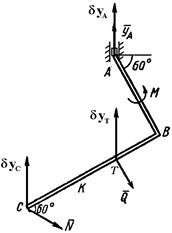
Для нахождения реакций  и
и 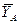 , последовательно помещаем в точке
, последовательно помещаем в точке 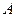 ползуны с горизонтальной (рис. 5.0, д) и вертикальной (рис. 5.0, е) направляющей, как это делалось ранее для точки
ползуны с горизонтальной (рис. 5.0, д) и вертикальной (рис. 5.0, е) направляющей, как это делалось ранее для точки 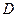 стержня. Придаем системе возможное поступательное перемещение и применяем ПВП.
стержня. Придаем системе возможное поступательное перемещение и применяем ПВП.
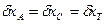 ,
,
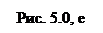
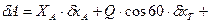
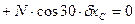 . (5)
. (5)
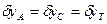 ,
,
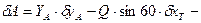
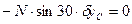 . (6)
. (6)
Из (5) и (6) вычисляем 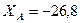 кН,
кН, 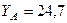 кН.
кН.
Ответ: 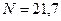 кН,
кН, 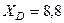 кН,
кН,  кН,
кН, 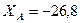 кН,
кН, 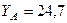 кН,
кН, 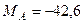
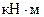 . Знаки минус указывают, что силы
. Знаки минус указывают, что силы 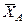 ,
, 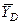 и момент
и момент 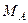 направлены противоположно показанным на рисунках. Ответ совпадает с решением примера 1.
направлены противоположно показанным на рисунках. Ответ совпадает с решением примера 1.
Date: 2015-09-24; view: 646; Нарушение авторских прав