Задание 4. Исследование движения механических систем

С помощью методов аналитической механики

Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3–6, прикрепленных к этим нитям, и невесомого блока (рис. 4.0–4.9, табл. 6). Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом 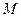, приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны: 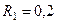м, 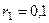м, а шкива 2 – 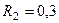м, 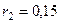м; их радиусы инерции относительно осей вращения равны соответственно 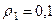м и м.

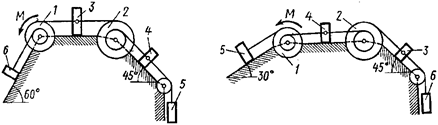
Рис. 4.0 Рис. 4.1

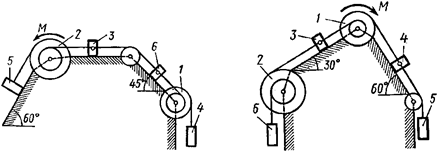
Рис. 4.2 Рис. 4.3

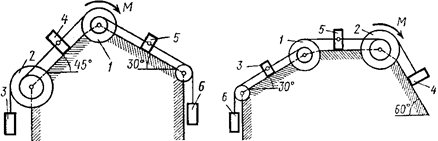
Рис. 4.4 Рис. 4.5

Рис. 4.6 Рис. 4.7

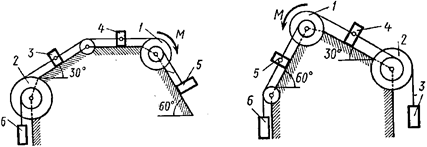
Рис. 4.8 Рис. 4.9

Пренебрегая трением, найти ускорение груза, имеющего больший вес; веса шкивов и грузов заданы в таблице. Грузы, веса которых равны нулю, на чертеже можно не изображать (шкивы 1, 2 изображать всегда как части системы).

Таблица 6

Номер условия							,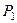

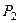
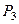
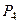
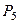
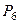
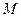Указания. Задание 4 решается с помощью двух методов аналитической механики – общего уравнения динамики (принципа Даламбера-Лагранжа) и уравнений Лагранжа II рода (см. приложение И).

При решении с помощью общего уравнения динамики надо присоединить к действующим на систему силам соответствующие силы инерции. Учесть при этом, что для однородного тела, вращающегося вокруг своей оси симметрии (шкива), система сил инерции приводится к паре с моментом , где 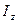– момент инерции тела относительно оси вращения, 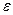– угловое ускорение тела; направление противоположно направлению 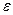. Ход решения задачи приведен на примере 4.

Решая задачу методом уравнений Лагранжа, надо учесть, что система имеет одну степень свободы, ее положение определяется одной обобщенной координатой и для нее должно быть составлено одно уравнение движения. В задачах, где требуется найти ускорение груза 3 (4, 5 или 6), за обобщенную координату удобно принять координату 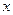, характеризующую перемещение этого груза. Для составления уравнения Лагранжа необходимо найти кинетическую энергию системы и выразить все входящие в нее скорости через обобщенную скорость , а затем вычислить обобщенную силу . Для этого надо сообщить системе возможное (малое) перемещение, при котором выбранная координата 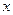получит приращение 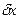, и составить уравнение работ всех сил на этом перемещении. Коэффициент при 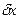в выражении элементарной работы и будет искомой обобщенной силой. Дальнейший ход решения задачи разъяснен в примере 5.

Date: 2015-09-24; view: 550; Нарушение авторских прав