
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример 1. На угольник ( ), конец которого жестко заделан, в точке опирается стержень (рис
|
|
На угольник  (
(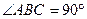 ), конец
), конец 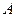 которого жестко заделан, в точке
которого жестко заделан, в точке 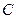 опирается стержень
опирается стержень 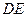 (рис. 1.10, а). Стержень имеет в точке
(рис. 1.10, а). Стержень имеет в точке 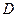 неподвижную шарнирную опору и к нему приложена сила
неподвижную шарнирную опору и к нему приложена сила 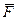 , а к угольнику – равномерно распределенная на участке
, а к угольнику – равномерно распределенная на участке 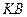 нагрузка интенсивности
нагрузка интенсивности 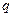 и пара с моментом
и пара с моментом 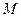 .
.
Дано: 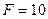 кН,
кН, 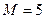
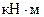 ,
, 
 ,
,  м.
м.
Определить: реакции в точках 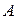 ,
, 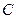 ,
, 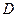 .
.
Решение:
1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня 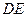 (рис. 1.10, б). Проведем координатные оси
(рис. 1.10, б). Проведем координатные оси  и изобразим действующие на стержень силы: силу
и изобразим действующие на стержень силы: силу 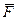 , реакцию
, реакцию 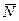 , направленную перпендикулярно стержню, и составляющие
, направленную перпендикулярно стержню, и составляющие 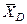 и
и 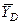 реакции шарнира
реакции шарнира 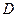 . Для полученной плоской системы сил составляем три уравнения равновесия:
. Для полученной плоской системы сил составляем три уравнения равновесия:

Рис. 1.10
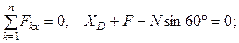 (1)
(1)
 (2)
(2)
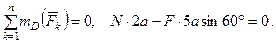 (3)
(3)
2. Рассмотрим равновесие угольника (рис. 1.10, в). На него действуют сила давления стержня 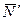 , направленная противоположно реакции
, направленная противоположно реакции 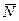 , равномерно распределенная нагрузка, которую заменяем силой
, равномерно распределенная нагрузка, которую заменяем силой 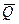 , приложенной в середине участка
, приложенной в середине участка 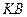 (
( кН), пара сил с моментом
кН), пара сил с моментом 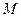 и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими
и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими 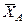 и
и 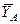 , и моментом
, и моментом 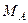 . Для этой плоской системы сил составляем уравнения равновесия:
. Для этой плоской системы сил составляем уравнения равновесия:
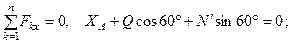 (4)
(4)
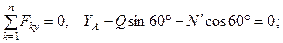 (5)
(5)
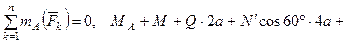
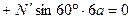 . (6)
. (6)
При вычислении момента силы 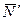 разлагаем ее на составляющие
разлагаем ее на составляющие 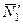 и
и  и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (1)–(6), найдем искомые реакции. При решении учитываем, что численно
и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (1)–(6), найдем искомые реакции. При решении учитываем, что численно  в силу равенства действия и противодействия.
в силу равенства действия и противодействия.
Ответ: 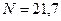 кН,
кН, 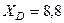 кН,
кН,  кН,
кН, 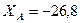 кН,
кН, 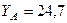 кН,
кН, 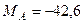
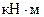 . Знаки минус указывают, что силы
. Знаки минус указывают, что силы 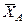 ,
, 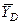 и момент
и момент 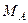 направлены противоположно показанным на рисунках.
направлены противоположно показанным на рисунках.
Date: 2015-09-24; view: 624; Нарушение авторских прав