
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вынужденные электромагнитные колебания
|
|
Вынужденными называются такие колебания, которые происходят в колебательной системе под влиянием внешнего периодического воздействия.
 Рассмотрим процессы, протекающие в электрическом колебательном контуре (рис. 1), присоединенном к внешнему источнику, ЭДС которого изменяется по гармоническому закону
Рассмотрим процессы, протекающие в электрическом колебательном контуре (рис. 1), присоединенном к внешнему источнику, ЭДС которого изменяется по гармоническому закону
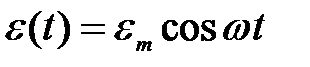 ,
,
| e (t) |
| L |
| C |
| R |
w – циклическая частота ЭДС.
Обозначим через UC напряжение на конденсаторе, а через i - силу тока в контуре. В этом контуре кроме переменной ЭДС e (t) действует еще ЭДС самоиндукции eL в катушке индуктивности.
ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока в контуре
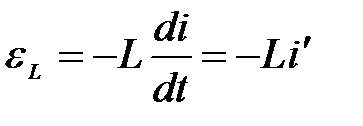 .
.
Для вывода дифференциального уравнения вынужденных колебаний возникающих в таком контуре используем второе правило Кирхгофа
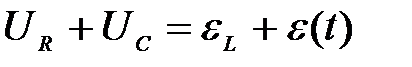 .
.
Напряжение на активном сопротивлении R найдем по закону Ома
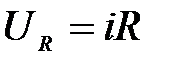 .
.
Cила электрического тока равна заряду протекающему за единицу времени через поперечное сечение проводника
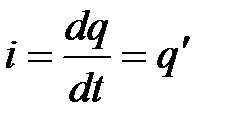 .
.
Следовательно
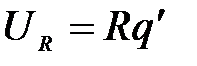 .
.
Напряжение UC на конденсаторе прямо пропорционально заряду на обкладках конденсатора
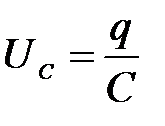 .
.
ЭДС самоиндукции можно представить через вторую производную от заряда по времени
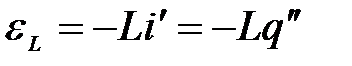 .
.
Подставляя напряжения и ЭДС во второе правило Кирхгофа
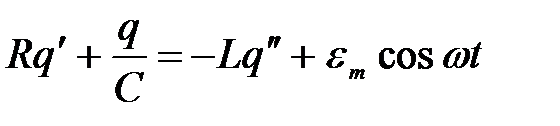 .
.
Разделив обе части этого выражения на L и распределив слагаемые по степени убывания порядка производной, получим дифференциальное уравнение второго порядка
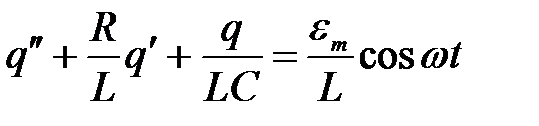 .
.
Введем следующие обозначения и получим
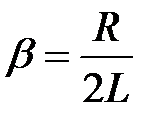 – коэффициент затухания,
– коэффициент затухания,
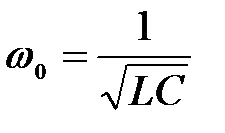 – циклическая частота собственных колебаний контура.
– циклическая частота собственных колебаний контура.
Date: 2015-09-24; view: 650; Нарушение авторских прав