Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Затухающие механические колебания
|
|
Свободные колебания реальных механических систем всегда затухают. Затухание возникает в основном из-за трения, сопротивления окружающей среды и возбуждения в ней упругих волн.
| e |
| Mсопр |
| Mупр |
| Z |
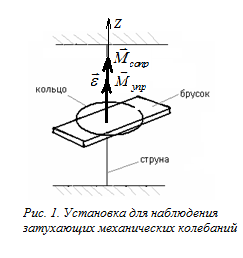совершающую крутильные затухающие колебания. Она представляет из себя брусок, подвешенный на струне, концы которой закреплены. На брусок для увеличения момента инерции может быть положено кольцо. После отклонения бруска на небольшой угол j от положения равновесия система будет совершать свободные крутильные колебания.
Получим дифференциальное уравнение затухающих крутильных колебаний. Чтобы выяснить, как изменяется со временем угол j (t) запишем основной закон динамики вращательного движения
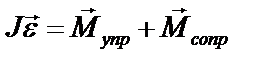, (1)
где: J – момент инерции бруска,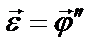 
– угловое ускорение,
– момент сил упругости,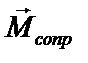 
– момент сил сопротивления.
Уравнение (1) спроектируем на ось OZ
,
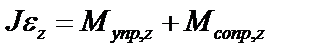где: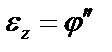 
– проекция углового ускорения,
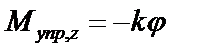– проекция силы упругости,
k – коэффициент упругости,
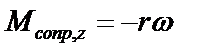– проекция силы сопротивления (эта формула справедлива для малых скоростей вращения),
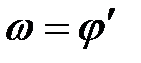– угловая скорость,
r – коэффициент сопротивления.
Уравнение (1) в скалярной форме примет вид
,
.
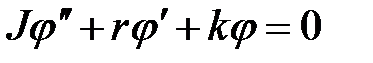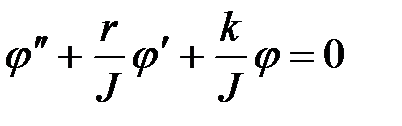Обозначим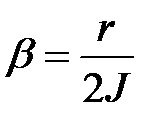 
– коэффициент затухания и 
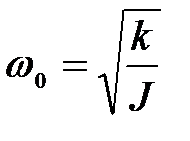– циклическая частота собственных колебаний, получим дифференциальное уравнение затухающих колебаний
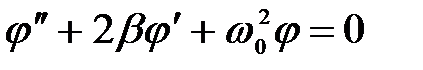(2)
Решением уравнения (2) при малом затухании w 0 > b является уравнение затухающих колебаний
(3) Амплитуда затухающих колебаний зависит от времени
,
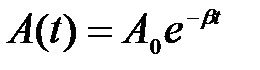здесь А 0 – амплитуда в начальный момент времени t = 0.
| j |
| t |
| A 0 e–bt |
Рис.2.
График затухающих колебаний.
Циклическая частота затухающих колебаний меньше собственной частоты
.
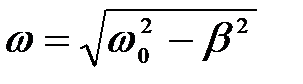Date: 2015-09-24; view: 1009; Нарушение авторских прав