Гармонических колебаний маятника

(физического и математического)

На рис. 1 показано сечение 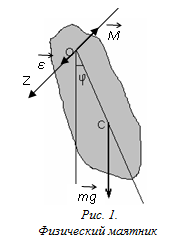физического маятника плоскостью, перпендикулярной к оси вращения и не проходящей через центр масс С. Расстояние ОС равно d.

При отклонении маятника от положения равновесия на угол j, под действием силы тяжести возникает вращающий момент сил , который стремится вернуть маятник в положение равновесия. Момента сил равен

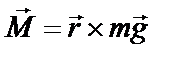, (1)

где: 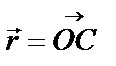– радиус-вектор, проведенный из точки подвеса маятника О в центр масс С,

т – масса маятника,

g – ускорение свободного падения.

Если уравнение (1) спроектировать на ось OZ параллельную оси вращения, то получится

,

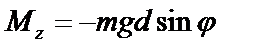где знак минус показывает, что момент силы тяжести стремится вернуть маятник в положение равновесия.

При малом угле φ с хорошей точностью значение синуса можно заменить на значение угла, при условии, что угол выражен в радианах

.

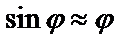Например, сравним sin 5^o» 0,087156 и . Видно, что разница составляет Δ = 0,00011. Таким образом, если угол φ < 5^o и выражен в радианах, то погрешность такой замены Δ < 10^–4.

При малых углах отклонения момент силы примет вид

. (2)

Для вывода закона движения маятника используем основной закон динамики вращательного движения

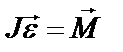, (3)

где J – момент инерции маятника относительно оси OZ,

– угловое ускорение.

Cпроектируем (см. рис. 1) уравнение (3) на ось OZ параллельную оси вращения

,

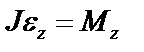где 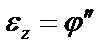, и подставим M_z из (2), тогда

.

Поделив на J, получим

.

Введем обозначение для циклической частоты колебаний ω ₀

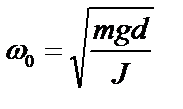. (4)

Получили дифференциальное уравнение гармонических колебаний

. (5)

Решением дифференциальное уравнение гармонических колебаний является уравнение гармонических колебаний.

, (6)

где: j – угол отклонения маятника,

А – амплитуда колебаний,

a = (w ₀ t + a ₀) – фаза колебаний,

a ₀ – начальная фаза, т.е. значение фазы в начальный момент времени t = 0,

w ₀ – циклическая частота колебаний,

t – время.

Вывод. При малых углах отклонения маятника (φ < 5^o), можно считать приближенно, что маятник совершает гармонические колебания.

Период колебаний физического маятника

. (7)

Для математического маятника формулу циклической частоты и периода можно получить из (4) и (7), если рассматривать математический маятник как частный случай физического маятника, у которого вся масса сосредоточена в центре масс С на расстоянии d = l от точки подвеса (момент инерции материальной точки J = ml ²). Тогда из (4) и (7) следует

(8)

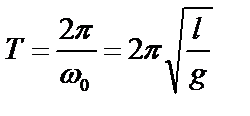(9)

Из сопоставления формул (7) и (9) получается, что математический маятник с длиной 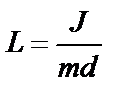будет иметь такой период колебаний, как и данный физический маятник. Величину L называют приведенной длиной физического маятника.

Приведенная длина физического маятника равна длине математического маятника, имеющего такой же период колебаний как у данного физического маятника

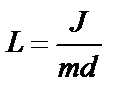. (10)

Date: 2015-09-24; view: 653; Нарушение авторских прав