Затухающие электромагнитные колебания

Рассмотрим собственные колебания в контуре с сосредоточенными параметрами. Емкость С, индуктивность L и активное сопротивление R образуют (рис. 2) последовательный колебательный контур (RLC контур).

Будем считать, что электрические процессы в контуре квазистационарны. Это значит, что мгновенное значение силы тока i одно и то же в любом месте контура и к мгновенным значениям электрических величин можно применять правила Кирхгофа.

Согласно второму правилу Кирхгофа алгебраическая сумма напряжений в любом замкнутом контуре равна алгебраическая сумме ЭДС, в этом контуре. В нашем случае сумма напряжений на конденсаторе и на активном сопротивлении равна ЭДС самоиндукции, которая возникает за счет изменения тока в катушке при перезарядке конденсатора

,

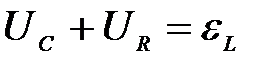где 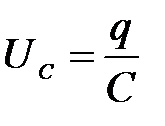– напряжение на конденсаторе,

– напряжение на активном сопротивлении,

– ЭДС самоиндукции в катушке.

Используем определение силы тока

.

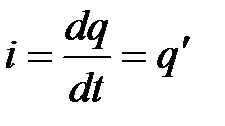Закон Кирхгофа примет вид

.

Разделим обе части этого уравнения на L

.

Введем следующие обозначения

– коэффициент затухания,

– циклическая частота собственных колебаний контура.

Получили дифференциальное уравнение затухающих колебаний, описывающее изменение со временем заряда на обкладках конденсатора в RLC контуре

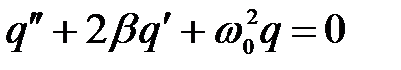(1)

Это однородное линейное дифференциальное уравнение второго порядка с обыкновенными производными и с постоянными коэффициентами. Решение этого уравнения имеет различный вид в зависимости от соотношения между коэффициентам.

1) Если w ₀ > b, то решением уравнения (1) является уравнение затухающих колебаний

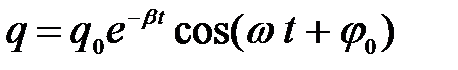, (2)

где: q ₀ – заряд конденсатора в начальный момент времени,

j ₀ – начальная фаза.

Значения q ₀ и j ₀ определяются из начальных условий.

Амплитуда затухающих колебаний зависит от времени и убывает со временем по экспоненциальному закону

.

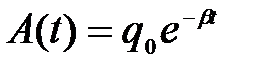Циклическая частота затухающих колебаний меньше собственной частоты

.

Период затухающих колебаний всегда больше периода собственных колебаний

.

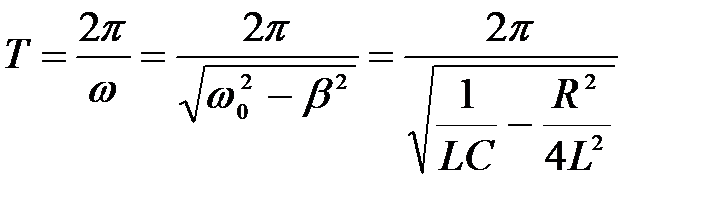Разделив (2) на электроемкость конденсатора С, получим напряжение наконденсаторе

.

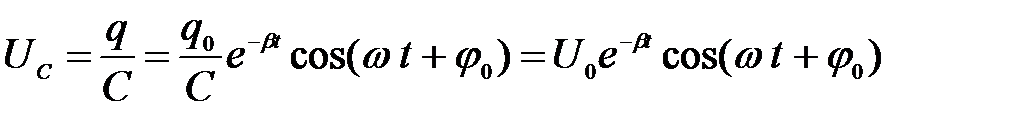Чтобы найти силу тока, продифференцируем (2) по времени

,

.

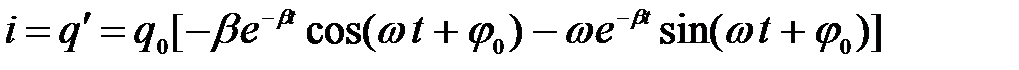Умножим и разделим это выражение на

.

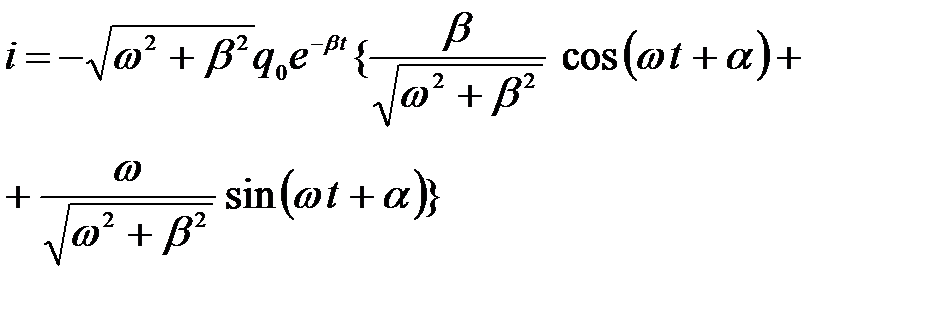Введем угол a, определяемый условиями (рис.4)

,

.

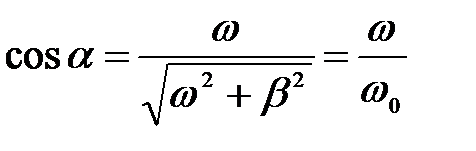Тогда можно записать

,

.

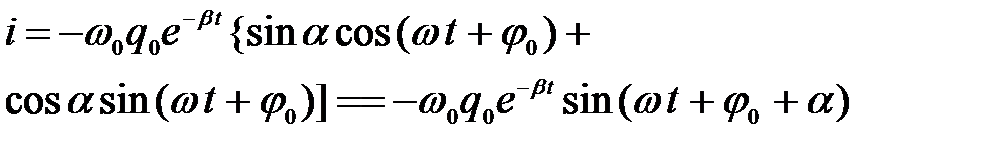Поскольку cos a > 0, а sin a > 0, то 0 < a < p /2.

Таким образом, при наличии в контуре активного сопротивления ток опережает по фазе напряжение на конденсаторе более чем на p /2 и менее чем на p (при R = 0 на p /2).

График затухающих колебаний заряда q изображен на рис. 5. Графики для напряжения и силы тока имеют аналогичный вид.

2) Пусть сопротивление контура велико, так что b > w ₀. В этом случае частота затухающих колебаний будет мнимой

,

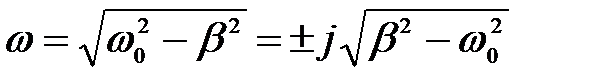где 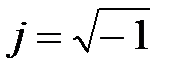– мнимая единица.

Это значит, что электрических колебаний в контуре не будет. В этом случае решение дифференциального уравнения (1) имеет вид апериодического процесса

,

, ,

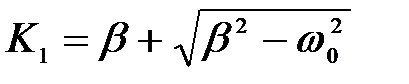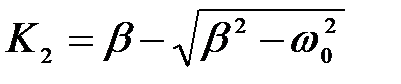где А ₁ и А ₂ постоянные, так как b > w ₀, то К ₁ и К ₂ оба вещественны и положительны.

Значения постоянных определяются начальными условиями задачи

,

.

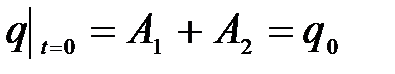Это дает

, .

После чего решение принимает вид:

.

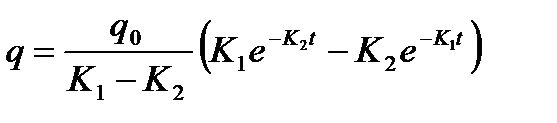На рис. 6 изображены графически оба слагаемых этой формулы (пунктир) и их сумма (сплошная линия). Вместо колебаний происходит апериодический разряд конденсатора. Если сопротивление контура очень велико, так что b >> w ₀, то К ₁ >> К ₂ и в последнем выражении можно пренебречь вторым слагаемым по сравнению с первым, а в знаменателе – К ₂ по сравнению с К ₁. Тогда .

Из сказанного видно, что для возникновения колебаний в RLC контуре необходимо, чтобы выполнялось условие w ₀ > b. Подставляем вместо w ₀ и b их значения, находим условие возникновения колебаний

или ,

.

Критическое сопротивление – это сопротивление контура, при котором колебательный процесс переходит в апериодический

.

Добротность колебательной системы характеризует ее способность сохранять энергию колебаний. Добротность пропорциональна отношению энергии W колебаний системы в произвольный момент времени t к убыли этой энергии за период D W

.

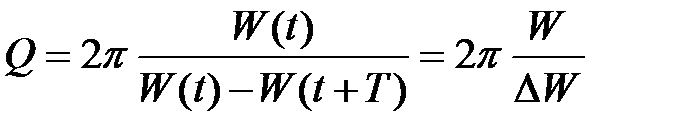Найдем связь между добротностью и логарифмическим декрементом затухания. При малых затуханиях w ₀ > b энергия меняется по закону

.

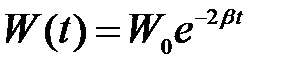Найдем изменение энергии за один период колебаний

,

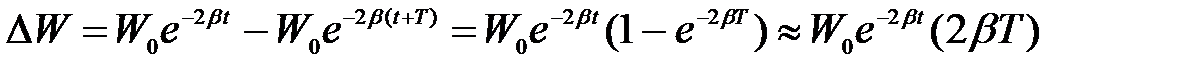т.к. , если .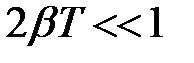

Подставим в добротность и учтем что d = bТ

.

Добротность обратно пропорциональна логарифмическому декременту затухания или пропорциональна числу колебаний N_e, по прошествии которых амплитуда убывает в е = 2,718 раз

.

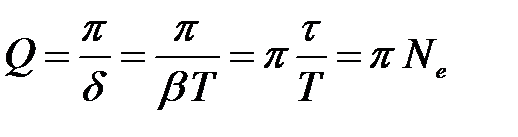Date: 2015-09-24; view: 2508; Нарушение авторских прав