В амплитудную
Преобразование частотной модуляции в амплитудную может быть выполнено с помощью любой линейной электрической цепи, обладающей комплексной, зависящей от частоты, передаточной функцией K (j ω). Требуемая зависимость выражена особенно ярко у интегрирующей или дифференцирующей цепи, резонансной избирательной цепи и т. д.
Вызывая изменение амплитуды, зависящее от частоты, линейная цепь с коэффициентом передачи K (j ω) и линейной фазочастотной характеристикой не изменяет частоты колебания u c(t), поэтому на выходе ее получается колебание, изменяющееся одновременно по частоте и по амплитуде. Это обстоятельство не препятствует осуществлению амплитудного детектирования, т.к. для относительно узкополосных сигналов колебание u вых(t) на выходе амплитудного детектора определяется только амплитудной модуляцией и практически не зависит от изменения частоты колебания.
Рассмотрим преобразование частотной модуляции в амплитудную модуляцию с помощью резонансной избирательной цепи с передаточной функцией резонансного контура
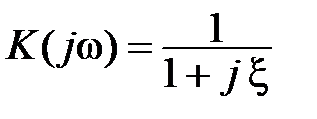 , (4.1) , (4.1)
где ξ – расстройка, 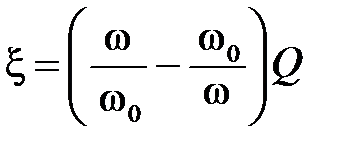 ; ω0– резонансная частота контура; Q – добротность контура. ; ω0– резонансная частота контура; Q – добротность контура.
Схема частотного детектора на расстроенном контуре приведена на рис. 4.1. Входной высокочастотный сигнал u c(t) поступает с избирательного контура усилительного каскада усилителя промежуточной частоты, к которому подключен LC -контур частотного детектора. Выход LC -контура соединен с амплитудным детектором, нагрузочной цепью которого является параллельное соединение конденсатора C ни резистора R н. К выходу амплитудного детектора подключается входной каскад усилителя низкой частоты.
На рис. 4.2 показано формирование закона изменения амплитуды ЧМ-сигнала при гармонической форме модулирующего сообщения x (t) = cos(Ω t). На этом рисунке U aМ(t) – закон сопутствующей амплитудной модуляции. Контур LC имеет резонансную частоту ω0, и расстройка |ωc – ω0| выбирается так, чтобы получить максимальную крутизну преобразования. При расстройке, равной 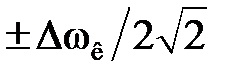 , АЧХ цепи имеет близкие к линейному нарастающий и спадающий участки, на которых выбирается рабочая точка. , АЧХ цепи имеет близкие к линейному нарастающий и спадающий участки, на которых выбирается рабочая точка.
| Рис. 4.1. Схема частотного детектора на расстроенном контуре
|
| Рис. 4.2. Формирование закона изменения амплитуды ЧМ-сигнала
на резонансном контуре
|
На практике частотные детекторы такого типа обычно реализуются на транзисторном избирательном усилителе с включением контура в коллекторную цепь. В этом случае комплексный коэффициент передачи принимает вид
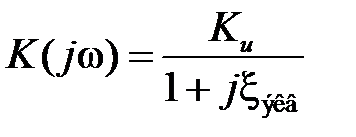 , (4.2) , (4.2)
где Ku – коэффициент усиления по напряжению транзисторного каскада; ξ экв– обобщенная расстройка, 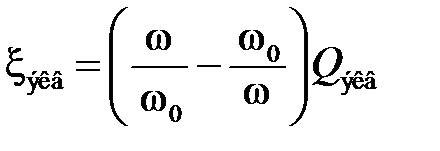 ; Q экв– эквивалентная добротность контура с учетом влияния сопротивления и емкости нагрузки. ; Q экв– эквивалентная добротность контура с учетом влияния сопротивления и емкости нагрузки.
В предположении линейности амплитудного детектора постоянная составляющая напряжения на его выходе будет равна
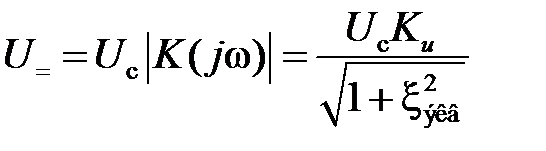 . (4.3) . (4.3)
Уравнение (4.3) описывает детекторную характеристику, которая по форме повторяет амплитудно-частотную характеристику резонансного усилителя. Крутизна детекторной характеристики в координатах U =, xэквизменяется по закону
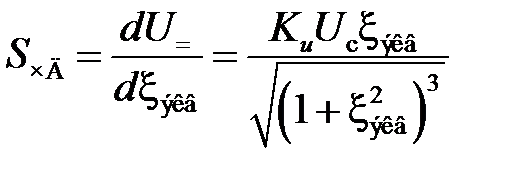 (4.4) (4.4)
и имеет максимальное значение при расстройке 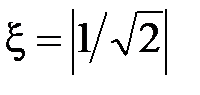 . .
Достоинством частотных детекторов с одиночным расстроенным контуром является простота реализации схемы и ее настройки. К недостаткам относится высокий уровень нелинейных искажений, обусловленных нелинейностью АЧХ резонансного усилителя.
Значительное уменьшение уровня нелинейных искажений может быть получено при использовании балансного частотного детектора с двумя расстроенными контурами (рис. 4.3).
Резонансные частоты 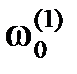 и и 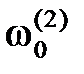 контуров L 1 C 1 и L 2 C 2 выбираются симметрично относительно средней частоты ω0, а постоянные составляющие напряжений на выходах амплитудных детекторов, подключенных к этим контурам, обеспечивают выходное напряжение как разность: контуров L 1 C 1 и L 2 C 2 выбираются симметрично относительно средней частоты ω0, а постоянные составляющие напряжений на выходах амплитудных детекторов, подключенных к этим контурам, обеспечивают выходное напряжение как разность:
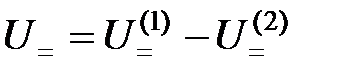 . .
В предположении равенства резонансных сопротивлений контуров и при одинаковых коэффициентах передачи амплитудных детекторов получим следующее уравнение детекторной характеристики:
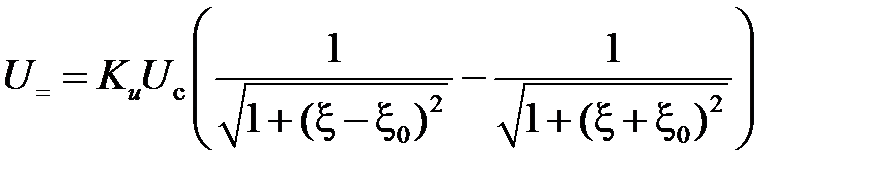 , (4.5) , (4.5)
где 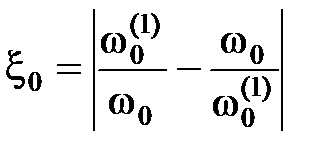 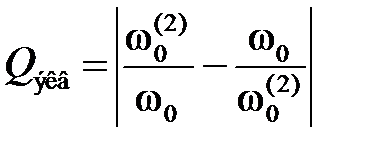 Q экв; Q экв; 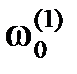 и и 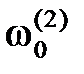 – резонансные частоты контуров L 1 C 1 и L 2 C 2. – резонансные частоты контуров L 1 C 1 и L 2 C 2.
| Рис. 4.4. Детекторная характеристика частотного детектора на двух
расстроенных контурах
|
| Рис. 4.3. Схема частотного детектора на двух расстроенных контурах
|
Крутизна детекторной характеристики (рис. 4.4) при x = 0 равна
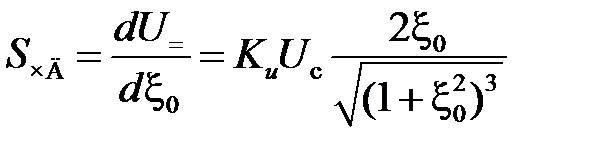 . (4.6) . (4.6)
Анализ выражения (4.6) показывает, что максимальное значение крутизны достигается при значении 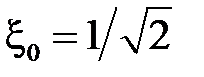 . однако наименьшая степень нелинейных искажений в диапазоне от . однако наименьшая степень нелинейных искажений в диапазоне от 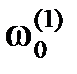 до до 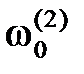 возможна при значении возможна при значении  . .
Так как величина U =зависит от уровня входного сигнала U c, перед частотным детектором необходим амплитудный ограничитель, устраняющий влияние изменений амплитуды U cна уровень выходного напряжения.
Date: 2015-09-24; view: 626; Нарушение авторских прав | Понравилась страница? Лайкни для друзей: |
|
|



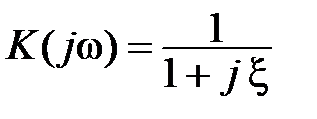 , (4.1)
, (4.1)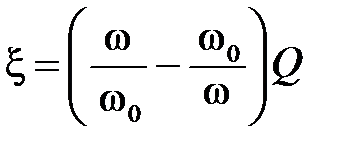 ; ω0– резонансная частота контура; Q – добротность контура.
; ω0– резонансная частота контура; Q – добротность контура.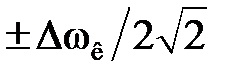 , АЧХ цепи имеет близкие к линейному нарастающий и спадающий участки, на которых выбирается рабочая точка.
, АЧХ цепи имеет близкие к линейному нарастающий и спадающий участки, на которых выбирается рабочая точка.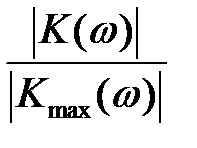
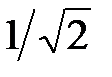
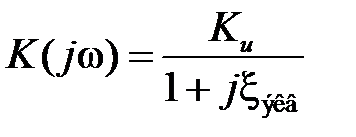 , (4.2)
, (4.2)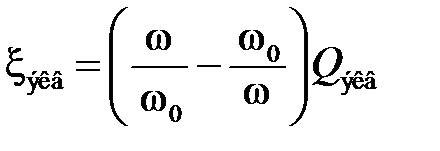 ; Q экв– эквивалентная добротность контура с учетом влияния сопротивления и емкости нагрузки.
; Q экв– эквивалентная добротность контура с учетом влияния сопротивления и емкости нагрузки.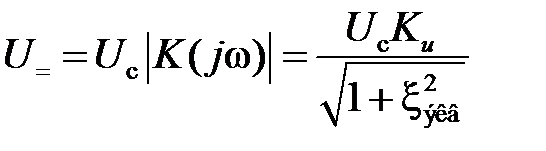 . (4.3)
. (4.3)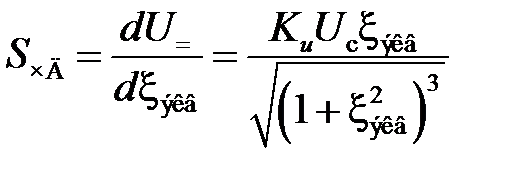 (4.4)
(4.4)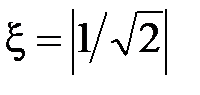 .
.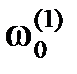 и
и 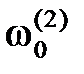 контуров L 1 C 1 и L 2 C 2 выбираются симметрично относительно средней частоты ω0, а постоянные составляющие напряжений на выходах амплитудных детекторов, подключенных к этим контурам, обеспечивают выходное напряжение как разность:
контуров L 1 C 1 и L 2 C 2 выбираются симметрично относительно средней частоты ω0, а постоянные составляющие напряжений на выходах амплитудных детекторов, подключенных к этим контурам, обеспечивают выходное напряжение как разность: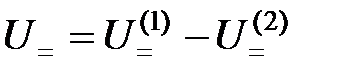 .
.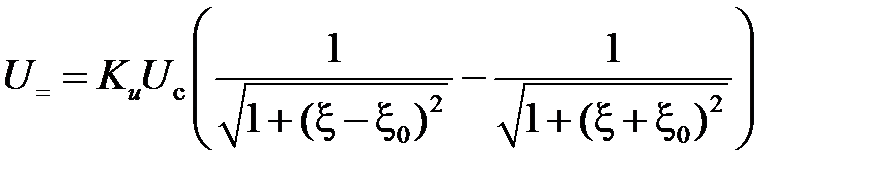 , (4.5)
, (4.5)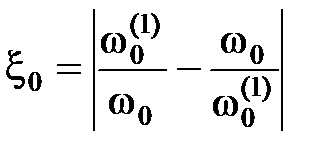
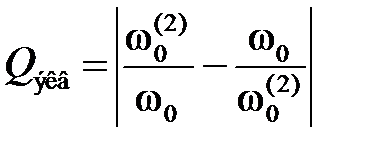 Q экв;
Q экв; 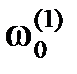 и
и 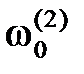 – резонансные частоты контуров L 1 C 1 и L 2 C 2.
– резонансные частоты контуров L 1 C 1 и L 2 C 2.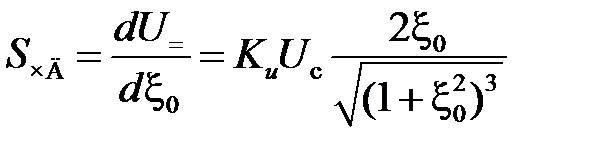 . (4.6)
. (4.6)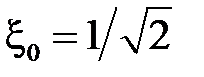 . однако наименьшая степень нелинейных искажений в диапазоне от
. однако наименьшая степень нелинейных искажений в диапазоне от 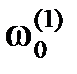 до
до 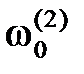 возможна при значении
возможна при значении  .
.