Определение и основные свойства циклических кодов

Важнейшим недостатком СБЛК, как отмечалось выше, является высокая трудоемкость их построения при длине кодовой последовательности n ≥ 31 двоичных символов и коррекции ошибок кратностью t_ош ≥ 3 двоичных символов. Поиск более простых принципов построения СБЛК привел к открытию нового широкого класса групповых линейных блоковых кодов, получивших название циклических кодов (ЦК). Основоположником ЦК является Прейндж [6]. Дальнейшее развитие теория построения ЦК получила в работах Боуза, Чоудхури, Хоквингейма, Файра, Рида-Соломона, Гоппы и др.

Циклические коды являются подклассом в классе линейных блоковых кодов, удовлетворяющих определенным требованиям. Свое название данные коды получили по причине того, что основной операцией построения кодовых последовательностей (F_i(x)) является цикл, а точнее циклическая перестановка двоичных символов разрешенных кодовых последовательностей [1-3,5-9].

В соответствии с [3,4,6] циклическим кодом называется линейный блоковый код, который представляет собой конечное множество, замкнутое относительно операции циклического сдвига кодовых последовательностей, образующих данный код. С математической точки зрения ЦК является идеалом в линейной коммутативной алгебре многочлена (полинома) n-го порядка по модулю двучлена хⁿ-1 над полем коэффициентов. Это означает, что кодовые последовательности ЦК имеют длину «n» двоичных кодовых символов и описываются полиномами степени (n-1), в которых коэффициентами при соответствующих степенях формальной переменной, обозначаемой через «х», являются двоичные символы кодовой последовательности. Формальная переменна «х», которая носит название оператора Хаффмана или оператора задержки и не оказывает никакого влияния на свойства кода. Таким образом, кодовую последовательность ЦК в общем виде можно записывать так:

F_i(x) = с_n-1∙x^n-1 + с_n-2∙x^n-2 +…+ с₁∙x¹ + с₀∙x⁰, (2.1)

где х – формальная переменная,

n-1, n-2, …, 1, 0 – показатели степеней, в которые возводятся основания кодов, и одновременно порядковые номера, которые занимают двоичные символы (разряды) кодовой последовательности, начиная со старшего и заканчивая нулевым;

c_i – коэффициенты формальной переменной, которые могут принимать или быть равными логической 1 (ненулевой член F_i(x)) или логического 0 (нулевой член F_i(x)). Например: F_i(x) = 1∙х⁴+0∙х³+0∙х²+1∙х¹+0∙х⁰=х⁴+х=10010.

Представление кодовых последовательностей в виде многочленов позволяет установить однозначное соответствие между ними и свести действия над кодовыми последовательностями к действиям над полиномами: умножение, сложение, деление и вычитание этих полиномов производится по обычным правилам алгебры, но коэффициенты с одинаковыми степенями формальной переменной «х» суммируются по модулю два. Например: F_i(x)=(х³+х²+1)∙F_j(x)=(x+1)=x⁴+х³+х²+x+1=x⁴+((1+1)mod2)∙х³+х²+x+1=x⁴+0·х³++х²+x+1= x⁴+х²+x+1.

Уточним сущность понятия циклического сдвига или циклической перестановки двоичных символов кодовой последовательности. Пусть F_i(x)=с_n-1x^n-1+c_n-2 x^n-2+…+c₁x¹+c₀x⁰, то циклический сдвиг на один разряд дает F_i(x)=с_n-1xⁿ+c_n-2x^n-1 +…+c₁x²+c₀x¹. Чтобы степень новой кодовой последовательности F_j(x) не превышала (n-1), член c_n-1xⁿ заменяется единицей, поэтому F_j(x)=с_n-2x^n-1+c_n-3x^n-2 +…+c₁x²+c₀x⁰+c_n-1x⁰.

Например, пусть F_i(x)=х⁵+х³+х²+х=0101110 при n=7 двоичных символов. (Заметим, что запись кодовой последовательности в виде многочлена, а затем перевод ее в двоичную форму записи, не всегда определяет длину кодовой последовательности «n». Например, при n=5, многочлен F(x) = x²+1=101, т.е. n=3, что неверно. В таких случаях надо дописать старшие нулевые символы, т.е. F(x)=x²+1=00101, что дает n=5 двоичным символам).

Сдвигаем F(x) на один разряд (символ) влево, и получаем F(x)=1011100=x⁶+x⁴+x³+x². Очевидно, что х¹(х⁵+х³+х²+х)=х⁶+х⁴+х³+х². Отсюда вытекает второе определение ЦК, а именно, циклический сдвиг двоичных символов разрешенной кодовой последовательности влево или вправо на один, два, …, (k-1) символов приводит к формированию разрешенной кодовой последовательности.

Таким образом, циклическую перестановку двоичных символов разрешенной кодовой последовательности можно рассматривать как умножение F(x) на «х» при первом сдвиге, на «х²» при втором сдвиге и т.д., что можно в общем виде записать или представить так:

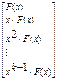(2.2)

Последний вывод можно рассматривать еще следующим образом: так как при сложении по модулю два двучлен хⁿ-1 можно записать как хⁿ=1, то замена хⁿ на 1 в произведении x∙F(x) дает новый многочлен, коэффициенты которого образуют новую разрешенную кодовую последовательность. Следовательно, в кодовой последовательности, имеющей длину «n» двоичных кодовых символов, степень полинома не может превышать n-1, так как в противном случае длина кодовой последовательности превысит «n», а поэтому хⁿ заменяется логической 1.

Таким образом можно сделать следующие выводы:

1. ЦК – это линейный код, который обладает свойством цикличности кодовых последовательностей, т.е. когда каждая разрешенная кодовая последовательность содержит ее циклическую перестановку;

2. ЦК относятся к групповым линейным кодам, если они образуются путем умножения каждой последовательности равнодоступного (простого) кода, выраженных в виде многочлена Q(x) с максимальной степенью (k-1), на некоторый полином Р(х) степени l=n-k. Приведение подобных членов производится по модулю два; порядок поля кодирования преобразуется с K_раз = 2^k до К_общ= 2ⁿ, но число разрешенных кодовых последовательностей кода при этом остается равным K_раз= 2^k, и они образуют циклическую подгруппу группы К_общ= 2ⁿ, отличающуюся тем, что все элементы подгруппы имеют общее свойство делимости на полином Р(х), получивший название образующего или порождающего полинома.

В соответствии с [1-9] в качестве образующего полинома используются полиномы, обладающие следующими свойствами:

– во-первых, образующий полином Р(х) должен быть делителем двучлена хⁿ+1;

– во-вторых, образующий полином не должен раскладываться на сомножители более низких степеней, и делиться без остатка на самого себя и на 1, т.е. на х⁰;

– в-третьих, максимальная степень образующего полинома должна быть равной l = n-k, т.е. соответствовать количеству проверочных символов используемого кода.

Так как ЦК являются дальнейшим развитием групповых СБЛК, то данные коды обладают всеми свойствами СБЛК, а также, имеют ряд дополнительных свойств.

К основным свойствам ЦК относятся:

1. Вес (w_к.п.) разрешенной кодовой последовательности ≥ d₀;

2. Вес проверочной части w_{пр.ч .} разрешенной кодовой последовательности ≥ d₀-1;

3. Сдвиг кодовых символов разрешенной кодовой последовательности влево или вправо на один, два, …, (k-1) символ вновь приводит к разрешенной кодовой последовательности. Если же при циклическом сдвиге всегда будет получаться новая кодовая последовательность, то такой код будет называться квазициклическим; данные коды имеют несколько большую корректирующую способность и сложность реализации, чем ЦК;

4. Разрешенная кодовая последовательность без ошибок F_р'(x) при делении на полином Р(х) дает нулевой остаток, т.е. F_p'(x)/P(x)=R(x)=0 и R(x) не равно 0 – при наличии ошибок;

5. Сумма по модулю два символов двух, трех, …, (k-1) разрешенных кодовых последовательностей вновь образует разрешенную кодовую последовательность;

6. Двучлен вида хⁿ+1 должен делиться на порождающий полином Р(х) без остатка (имеется ввиду обычная операция деления многочленов);

7. Если все операции над полиномами (кодовыми последовательностями) проводятся в двоичном поле Галуа (GF(2)), т.е. действия над коэффициентами полиномов осуществляются по модулю два, а умножение полиномов производится по модулю образующего полинома Р(х), то применение указанных операций не приводит к кодовым последовательностям, длина которых больше длины заданного кода, т.е. «n»;

8. Результат деления двучлена хⁿ+1 на образующий полином Р(х) дает полином, который носит название проверочного полинома и обозначается как h(x), т.е. h(x)=(хⁿ+1)/P(x) и который в теории и практике помехоустойчивого кодирования играет важную роль. Произведение h(x)·P(x)=хⁿ+1=0, а потому многочлены h(x) и P(x) рассматриваются как ортогональные и операция деления (хⁿ+1)/P(x) используется в основе построения алгоритмов декодирования;

9. Двучлен ЦК вида хⁿ-1 можно разложить на множители

хⁿ-1 = (х-1)(х^n-1+ х^n-2+…+1), (2.3)

которые можно использовать в качестве образующих полиномов ЦК с n=const, k=var и d₀=var.

Например, разложить двучлен хⁿ-1=х⁷-1 на множители вида (2.3) и определить образующие полиномы и параметры кодов.

Решение: двучлен х⁷-1 раскладывается на следующие многочлены:

х⁷-1 = (х-1)(х³+х²+1)(х³+х+1) (2.4)

Из данного выражения видно, что можно образовать шесть делителей для двучлена х⁷-1, путем комбинирования полученных трех сомножителей (2.3). Следовательно, для двучлена х⁷-1 существует шесть разных двоичных линейных ЦК со следующими образующими полиномами и параметрами:

Р₁(х)=(х-1)=(х+1); l=1, n=7, k=6, d₀=1 – простой код: l, k, n и t_исп (t_исп – кратность исправленных ошибок) – измеряется в двоичных символах;

P₂(x) = (x³+x²+1); l=3, n=7, k=4, d₀=3, t_исп=1;

P₃(x) = (x³+x²+1); l=3, n=7, k=4, d₀=3, t_исп=1;

P₄(x) = P₂(x)∙P₃(x)=(x⁴+x³+x²+1); l=4, n=7, k=3, d₀=4, t_исп=1;

P₅(x) = P₂(x)·P₃(x)=(x⁴+x²+x+1); l=4, n=7, k=3, d₀=4, t_исп=1;

P₆(x) = P₁(x)∙P₅(x)=(x⁶+x⁵+x⁴+ x³+x²+x+1); l=6, n=7, k=1, d₀=7, t_исп≤3.

ЦК, задаваемые образующими полиномами Р₁(х),Р₂(х) и Р₃(х), относятся к классу ЦК Хэмминга. ЦК, задаваемые полиномами Р₄(х),Р₅(х) и Р₆(х), являются двойственными кодами Хэимминга и называются кодами максимальной длины (КМД).

Известно [1-9], что корректирующая способность СБЛК существенно зависит от вида (структуры) образующего полинома, т.е. от количества ненулевых членов данного полинома и его максимальной степени l = n-k.

В соответствии с этим можно отметить следующие свойства ЦК:

а) обнаруживающих ошибки:

– ЦК, образующий полином которого имеет более одного члена и не имеет общего множителя «х», обнаруживает все одиночные ошибки и любое нечетное число ошибок. Простейшим образующим полиномом ЦК, обладающим данными свойствами, является полином вида Р(х)=1+х;

– ЦК, образующий полином которого имеет вид Р(х)=1+х^c, обнаруживает любое нечетное число ошибок. Доказательство этого утверждения становится ясным, если образующий полином представить в следующем виде Р(х)=1+х^c =(1+х)·(1+х+х²+…+х^c-1).

б) обнаруживающих и корректирующих ошибки:

– ввиду того, что полином Р(х)=1+х^c нацело делится на 1+х, то согласно предыдущему свойству ЦК обеспечивает обнаружение любого нечетного количества ошибок;

– ЦК, образующий полином которого имеет максимальную степень l=n-k, обнаруживает любой пакет ошибок длиной t_{пак.обн.}=l и менее двоичных символов или корректирует пакеты длиной t_{пак.обн.}=l/2 двоичных символов;

– количество пакетов длиной l+1, не обнаруживаемых ЦК, составляет 1/2^l-1 части всех пакетов (l+1) двоичных символов. Количество пакетов ошибок длиной более l+1, необнаруживаемых ЦК, составляет часть всех пакетов ошибок длиной от (l+2) до «n» двоичных символов включительно. Доказательство данных утверждений свойств ЦК можно найти в [1,8,9].

Date: 2015-09-22; view: 1016; Нарушение авторских прав