Назначение и способы построения проверочной матрицы циклического кода

Проверочные матрицы ЦК могут использоваться для выбора как способов кодирования информации, так и алгоритмов декодирования. Проверочные матрицы ЦК могут быть построены с использованием порождающей матрицы G_k,n(х), единичной матрицы проверок и проверочного полинома h(x).

Сущность способа построения проверочной матрицы H_l,n(x) с использованием канонической порождающей матрицы G_k,n(х) состоит в следующем.

Пусть задана следующая каноническая матрица ЦК с параметрами (n,k,d₀)=(7,4,3) вида:

G_4,7(х) = 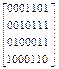H_3,7(х) = 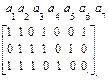(2.7)

Первый столбец проверочной матрицы H_3,7(x) для данного кода записываем, используя проверочные символы первой строки G_4,7(x), второй, третий и четвертый столбцы H_3,7(x) формируем путем записи проверочных символов второй, третей и четвертой строк G_4,7(x), а далее записываем три столбца единичной подматрицы. В результате получаем следующую проверочную матрицу (2.7). Ненулевые символы строк проверочной матрицы определяют позиции информационных символов, участвующие в формировании проверочных уравнений. Так для простроенной проверочной матрицы H_3,7(x) можно сформировать следующие три уравнения: b₁=a₁Åa₂Åa₄, b₂=a₂Åa₃Åa₄, b₃=a₁Åa₂Åa₃.

Принцип построения проверочной матрицы с использованием единичной подматрицы и остатков от деления аналогичен принципу построения порождающей матрицы. Количество остатков от деления xⁿ+1 на Р(х) должно быть равно количеству строк единичной подматрицы.

Сущность принципа построения проверочной матрицы ЦК с использованием проверочного полинома h(x) состоит в следующем. Первоначально определяем проверочный полином как отношение хⁿ+1 на Р(х), т.е. h(x)=xⁿ+1/P(x). Полученный полином переводим в двоичную форму записи, записываем в виде первой строки проверочной матрицы H_l,k(x) и дополняем нулями до количества столбцов, равное «n». Далее выполняем (l-1) циклический сдвиг двоичных символов первой строки.

Пример 2.3. Построить проверочную матрицу ЦК с параметрами (n,k,d₀)=(7,4,3), если Р(х)=х³+х²+1.

Решение:

1) определяем проверочный полином ;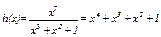

2) переводим в двоичную форму записи h(x)=11101;

3) записываем в виде первой строки H_3,7(х) и дополняем двумя нулевыми символами до n = 7

4) выполняем (l-1) = (3-1) = 2 циклических сдвига двоичных символов первой строки H_3,7(х) строим проверочную матрицу H_3,7(х) следующего вида:

5) далее можно сформировать проверочные уравнения вида (нумерация позиций двоичных символов строк проставлена вверху матрицы H_3,7(х)), b₁=a₁Åa₂Åa₃, b₂=a₂Åa₃Åa₄, b₃=a₃Åa₄Åa₅.

Date: 2015-09-22; view: 827; Нарушение авторских прав