Способ построения кодовых последовательностей с использованием порождающей матрицы

Кодовая последовательность ЦК при заданной порождающей матрице G_k,n(х) и заданном информационном блоке Q(x) формируется по правилу F(x)=Q(x)∙G_k,n(х), т.е. произведением вектора-строки Q(x), содержащего «k» информационных двоичных символов, на порождающую матрицу G(x) рангом (k ´ n).

При этом, если используется каноническая (приведенно-ступенчатая) G(x), то будут формироваться кодовые последовательности систематического разделимого ЦК. Порождающая матрица G(x) строится довольно просто, если задан образующий полином Р(х) и длина кодовой последовательности «n». Рассмотрим следующие примеры на матричное представление ЦК.

Пример 2.1. Сформировать кодовую последовательность ЦК с параметрами (n,k,d₀)=(10,5,5), если Р(х)=х⁵+х⁴+х²+1.

Решение: переводим Р(х) из записи в форме полинома в двоичную форму записи, Р(х)=х⁵+х⁴+х²+1=110101. Далее формируем первую строку матрицы G_5,10(х) следующим образом: двоичную последовательность 110101 дополняем справа четырьмя нулями; в результате получаем разрешенную кодовую последовательность вида 1101010000 длиной n=10 двоичных символов. Следующий шаг – выполнение (k-1)=(5-1)=4 циклических сдвига двоичных символов первой строки G(x).

В результате получаем следующую порождающую матрицу

G_5,10(х) = (2.5)

Этот способ построения порождающей матрицы G_5,10(х) можно рассмотреть со следующей позиции:

а) переводим Р(х) из записи в форме полинома в форму двоичной последовательности (можно и не переводить), т.е. Р(х)=х⁵+х⁴+х²+1=110101;

б) умножаем Р(х)=110101 на одночлен вида х^k-1, т. е. на 1000; в результате получаем первую строку или первую разрешенную кодовую последовательность 1101010000, а далее используем рассмотренную методику, т.е. циклический сдвиг двоичных символов первой строки (k-1) раз.

В общем случае построение порождающей матрицы G(x) ЦК с использованием образующего полинома можно записать так:

G(х) = 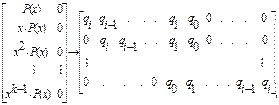(2.6)

где q=0;1 – коэффициенты образующего полинома, которые могут принимать либо 0, либо 1, 0 – нулевые символы, дополняющие каждую строку до значения «n» двоичных символов.

Формирование кодовой последовательности F(x), т. е. процесс кодирования информации с помощью G(x) осуществляется по правилу F(x)=Q(x)∙G(x): первый символ Q(x) умножаем на первый символ первого столбца G(x), второй символ Q(x) умножаем на второй символ первого столбца G(x) и суммируем по модулю два с первым результатом, третий символ Q(x) умножаем на третий символ первого столбца G(x) и суммируем по модулю два с предыдущим результатом и т.д. Затем первый символ Q(x) умножаем на первый символ второго столбца G(x) и далее все повторяется аналогично формированию первого кодового символа F(x).

Пример 2.2. Рассмотрим способ формирования кодовых последовательностей ЦК с использованием единичной матрицы и остатков от деления х^n-1/Р(х).

Для рассмотрения сущности формирования кодовых последовательностей ЦК используем данные предыдущего примера.

Так как k =5, то используем единичные векторы: Q₁(x)=10000, Q₂(x)=01000, Q₃(x)=00100, Q₄(x)=00010, Q₅(x)=00001. Записываем Q₁(x)…Q₅(x) в виде единичной подматрицы рангом (5 ´ 5).

G_5,10(х) =

Далее определяем проверочные символы каждой строки по следующей методике: делим х^n-1/Р(х) и берем остатки от деления для первой строки – от первого такта деления, т.е. R₁(x), для второй строки – после двух тактов деления, т.е. R₂(x) и т.д. Полученные символы дописываем к соответствующим строкам единичной подматрицы:

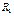= R₂(x)=11111, R₃(x)=01011, R₄(x)=00011 и R₅(x)=10011.

Формирование кодовых последовательностей осуществляется по правилу, приведенному в примере 2.1, т.е. F(x)=Q(x)∙G_5,10(x).

Date: 2015-09-22; view: 860; Нарушение авторских прав