Электрослабое взаимодействие

Электромагнитное и слабое взаимодействия объединены в единую теорию электрослабого взаимодействия Глэшоу-Вайнберга-Салама на основе калибровочной группы 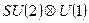. Наблюдение промежуточных векторных бозонов W⁺, W^-, Z⁰ на протон-антипротонных встречных пучках является прямым экспериментальным подтверждением данной теории. Характерной чертой теории является присутствие киральных фермионов (фермионные поля являются собственными векторами проекционных операторов 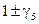), что проявляется как нарушение Р -инвариантности в слабых процессах.

Электрослабое взаимодействие - взаимодействие, в котором участвуют кварки и лептоны, излучая и поглощая фотоны или тяжелые промежуточные векторные бозоны W⁺, W^-, Z⁰. Электрослабое взаимодействие описывается квантовополевой калибровочной теорией с группой симметрии 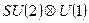со спонтанно нарушенной симметрией (С.Вайнберг и А. Салам 1967г.).

В исходной теории имеется три безмассовых векторных поля 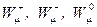соответствующие симметрии 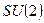с константой 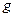и поле 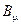связанное с симметрией 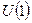с константой 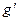. Исходная симметрия должна быть спонтанно нарушена так, чтобы получили массы кванты слабого взаимодействия 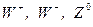, а квант электромагнитного поля (фотон) 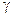остался безмассовым.

Два нейтральных поля 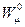, 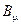соответствуют линейным комбинациям наблюдаемых физических поле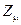й и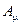

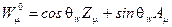
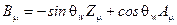(2.90)

где 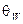- угол Вайнберга.

Минимальное число скалярных полей, приводящих к возникновению масс трех промежуточных бозонов, равно четырем. В качестве таковых выбирается комплексный дублет, т.е. вектор спинорного представления группы 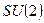: 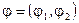и 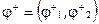, где + означает эрмитово сопряжение.

Исходный лагранжиан калибровочных и скалярных полей инвариантный относительно калибровочных преобразований с группой 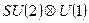имеет вид:

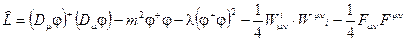(2.91)

первое слагаемое –динамическое,

второе слагаемое -массовый член, третье слагаемое – самодействие,

четвертое слагаемое -кинетическая энергия калибровочных полей,

пятое слагаемое -кинетическая энергия фотонного поля.

Здесь 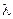>0-константа взаимодействия поля Хиггса; тензор напряженности фотонного поля 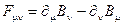, где 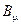- 4-векторный потенциал электромагнитного поля; 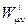-напряженность поля Янга-Миллса. Ковариантная производная определена выражением

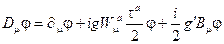
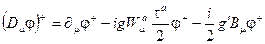, (2.92)

где 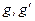-константы взаимодействия поля Хиггса с полями 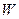и В, 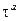- Матрицы Паули.

Явление (механизм) Хиггса осуществляется при отрицательных квадратах масс скалярных частиц 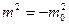< 0. Предполагается, что скалярное поле 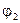приобретает ненулевое вакуумное среднее 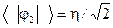. Скалярные поля переопределяются

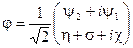
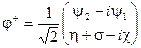(2.93)

Здесь физическими полями являются 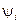, , 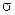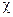. Подстановка переопределенных скалярных полей в лагранжиан приводит к появлению члена первой степени по полю .

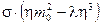Если вакуумное среднее поля 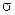равно нулю, то 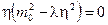. Решение 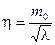нарушает симметрию. Коэффициенты при квадратах полей 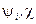равны 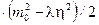, т.е.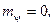 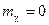, а у калибровочного поля 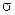появляется масса 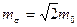. Безмассовые скалярные частицы уходят из физического спектра в результате явления Хиггса. При этом необходимо провести следующее калибровочное преобразование векторных потенциалов заряженных бозонов:

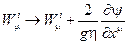(2.94)

Заряженные бозоны 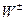приобретают массу 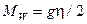, и Нейтральные поля 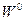и 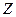образуют комбинацию

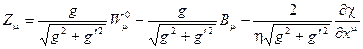(2.95)

причем нейтральный бозон 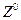приобретает массу 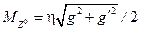. Угол Вайнберга связан с константами связи

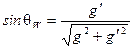, (2.96)

Таким образом, три безмассовых скаляра в результате механизма Хиггса включаются в массивные векторные поля. Из равенства заряда 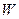элементарному заряду е получаемсвязь

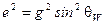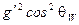= . (2.97)

Для описания взаимодействия векторных и скалярных полей с элементарными спинорами-лептонами и кварками вводятся лептонные мультиплеты

левые 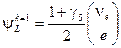и правые 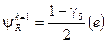, аналогично при 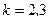для ,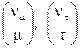

и кварковые мультиплеты

левые 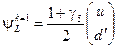, правые ,

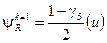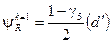
и аналогично при 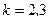для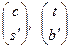

Штрихи у кварков 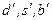означают комбинацию кварков 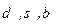определяемую через матрицу Кобаяси-Маскава.

Преобразование левых и правых компонент поля 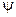подчиняется калибровочному преобразованию группы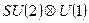

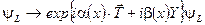
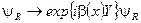(2.98)

Здесь 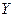-слабый гиперзаряд определенный соотношением

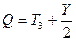(2.99)

где 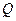-оператор заряда, являющийся генератором группы 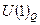, оператор гиперзаряда 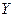генерирует группу .

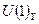Слабые токи описываются группой 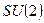с зарядами 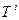, которые генерируют алгебру группы

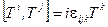. (2.100)

Окончательный вид электрослабого взаимодействия лептонов и кварков с векторными полями следующий

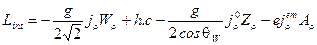(2.101)

где заряженный ток состоит из лептонного и кваркового

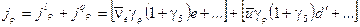, (2.102)

электромагнитный ток состоит из диагональных лептонных (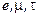), обычных кварковых 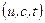и комбинационных кварковых токов

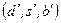
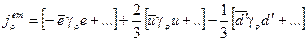(2.103)

нейтральный ток состоит из кваркового, комбинационного кваркового и электромагнитного токов

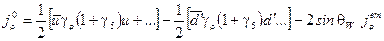. (2.104)

Калибровочная константа связи 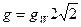. Масса заряженных векторных бозонов 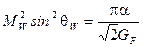, (2.105)

где константа электромагнитного взаимодействия .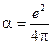

Таким образом, окончательный лагранжиан 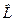стандартной модели (Вайнберга- Салама) электрослабого взаимодействия имеет вид см.табл.2.5

Табл.2.5

Лагранжиан стандартной модели (Вайнберга- Салама) электрослабого взаимодействия = = Кинетическая энергия и самодействие частиц полей , , + + Кинетическая энергия лептонов и кварков и взаимодействие лептонов и кварков с частицами полей , , +   + +   Взаимодействия и массы частиц полей , , и хиггсовской частицы Н + + Массы кварков и лептонов и взаимодействие кварков и лептонов с хигговской частицей Н.

Примечание:

Здесь индексом 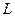обозначен левый фермионный (лептонный или кварковый) дублет, а индексом 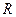-правый фермионный синглет.

Экспериментальным подтверждением электрослабой теории является:

открытие нейтральных токов в 1973г,

получение экспериментального значения угла Вайнберга ,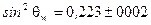

открытие векторных бозонов 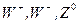в 1986г.,

открытие 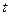-кварка в 1995г.

Экспериментальные данные, находящиеся в согласии с электрослабой теорией это: 1. данные по многочисленным распадам частиц (проверка взаимодействия заряженного тока с 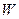-бозоном, 2.данные по нейтринным реакциям (проверка взаимодействия с 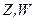-бозонами), 3.данные по массам и ширинам уровней самих векторных бозонов.

Основная проблема, требующая решения – изучение механизма нарушения исходной инвариантности. Главное- экспериментальное обнаружение хиггсовой скалярной частицы Н, электрослабая теория не предсказывает её массу (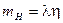, где 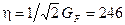Гэв значение константы поля 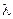Хиггса не известно). Активно обсуждается возможность поиска бозона Хиггса Н (электрический заряд 0,) в диапазоне 100 Гэв <М_н<1000 Гэв =1 Тэв, (наиболее вероятная между 114 Гэв и192 Гэв) которая будет исследована на новом протон-антипротонном суперколлайдере в ЦЕРНЕ (запущен в 2009 г) и работающем Тэватроне Лаборатории им Ферми. Другая важная проблема - это механизм нарушения СР - и Т -инвариантностей (экспериментально нарушения зарегистрирированы, но не известна причина их возникновения).

Date: 2015-09-05; view: 656; Нарушение авторских прав
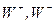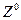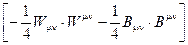
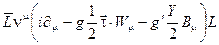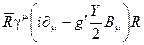
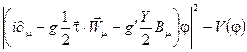