Спонтанное нарушение локальной калибровочной симметрии SU(2). Механизм Хиггса

Возьмем модельный лагранжиан слабого взаимодействия

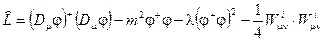(2.80)

где 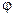есть изотопический спинор ( 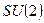-дублет комплексных скалярных полей)

, (2.81)

второе слагаемое массовое, третье слагаемое – самодействие скалярных полей, четвертое слагаемое –кинетическая энергия калибровочных полей.

Для инвариантности лагранжиана относительно локальных фазовых преобразований группы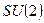

(2.82)

вводим ковариантные производные согласно примеру 4 формула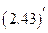

(2.83)

(2.84)

- напряженность поля Янга-Миллса

Возникает три калибровочных поля с дополнительно к четырем скалярным полям 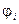(). согласно формуле .

В случае, когда <0 и 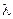>0 потенциал имеет минимум при конечном значении при котором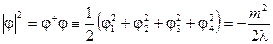

Множество точек, в которых потенциал принимает минимальное значение, инвариантно относительно преобразований группы 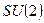. Выбирем точку минимума

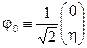, , которую обозначим . Это эквивалентно спонтанному нарушению 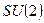- симметрии.

Разложим теперь 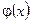в окрестности этого специально выбранного вакуума

(2.85)

подстановка этого выражения в исходный лагранжиан (2.80)приводит к выражению

(2.86)

Таким образом, из четырех скалярных полей 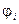остается только одно хиггсово поле .

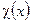Подставляя 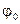в лагранжиан(2.86), выделяя второе слагаемое

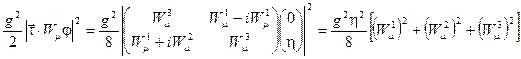(2.87)

и сравнивая его с массовым слагаемым для бозона получаем, что три калибровочных бозона обрели массу

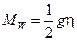. (2.88)

Сравнивая в следующем третьем слагаемом (2.86) член 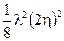и массовый член 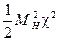получаем бозон Хиггса с массой

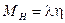, (2.89)

где Гэв, величина константы 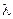не известна.

Отметим что, бозон Хиггса экспериментально не обнаружен (2009 г). Механизмом Хиггса называется механизм возникновения массы у калибровочного поля вследствие спонтанного нарушения симметрии.

Date: 2015-09-05; view: 439; Нарушение авторских прав