Сильное взаимодействие. Квантовая хромодинамика (КХД). Лагранжиан КХД

Сильное взаимодействие – взаимодействие, в котором участвуют адроны. Оно является короткодействующим: радиус действия ~ 10^{-13 см. В обычном веществе сильное взаимодействие создает прочную связь между нуклонами в ядрах (энергия связи ~ 8 Мэв/нуклон) и отвечает за стабильность ядер. При высоких энергиях сталкивающихся протонов меньших 1 Гэв сильное взаимодействие приводит к рождению пи-мезонов, при энергиях больших 1 Гэв рождаются странные частицы, очарованные, красивые мезоны и множество резонансов, см табл.3 Приложения.}

Квантовая хромодинамика (КХД) – квантовополевая теория сильного взаимодействия цветных кварков и цветных глюонов. Сильное взаимодействие осуществляется путем обмена глюонов между кварками. Теория построена на основе принципа локальной калибровочной инвариантности относительно преобразований в трехцветном комплексном пространстве внутренних симметрий (SU)_c. КХД возникла в начале 70г. ХХ века в результате синтеза представлений о цвете кварков, партонной картины глубоко неупругого взаимодействия и математического аппарата неабелевых калибровочных полей.

Лагранжиан КХД строится по образцу лагранжиана КЭД (для простоты принято, что у кварка один аромат и три цвета):

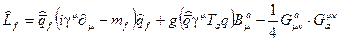. (2.49)

здесь первое слагаемое состоит из кинетической энергии частиц кваркового поля и массового члена частицы,

второе слагаемое это взаимодействие частиц кваркового поля с частицами глюонного поля,

последнее слагаемое - кинетическая энергия частиц глюонного поля.

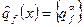- оператор кваркового поля Дирака аромата f =1,2…6.,c цветом α =1,2,3. черта сверху означает дираковское сопряжение.

- токовая масса кварка данного аромата f.

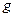-константа цветового взаимодействия (используется система )

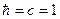, где 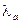матрицы (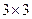) Гелл-Мана а =1,2,…8.

Коммутатор матриц ,

где -действительные константы группы SU(3)_c.

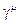-матрицы Дирака, .

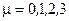- четырехмерный векторный потенциал глюонного поля (поля Янга-Миллса).

. –тензор напряженности поля Янга-Миллса.в формуле (2.44) другие обозначения

Матрицы 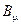и 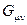могут быть разложены по восьми генераторам группы SU (3) _c в фундаментальном представлении , где 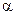, 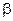= 1, 2, 3 цветовой заряд. 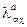- матрицы Гелл-Манна (). 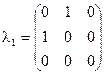, 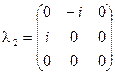…см. (2.128)

, .

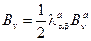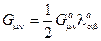Калибровочно-инвариантный тензор напряженности восьми глюонного полей имеет вид

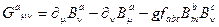(2.50)

Эти генераторы группы соответствуют квантам сильного взаимодействия, т.е.восьми безмассовым двуцветным глюонам: пример- g ₁^кз(«красно-зеленый глюон»)

Такой лагранжиан КХД является инвариантным относительно калибровочных преобразований кварковых полей

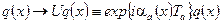
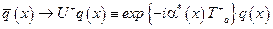, (2.51) и глюонных полей

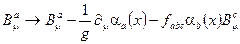(2.52)

Если переписать лагранжиан КХД в символической форме

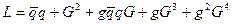. (2.53)

Первые три члена имеют имеют аналоги в КЭД. Первое слагаемое кинетическая энергия свободного движения кварков, второе-глюонов, третье слагаемое – кварк-глюонное взаимодействие, четвертое слагаемое -самодействие трех глюонов, пятое слагаемое -самодействие четырех глюонов. (См рис.2.13. Диаграммы Феймана). Уравнение Эйлера Лагранжа для полей Янга-Миллса см формулу (2.43).

Date: 2015-09-05; view: 756; Нарушение авторских прав