Примеры. В безвоздушном пространстве снаряд, выпущенный из пушки под некоторым углом к горизонту, будет двигаться по параболе под действием силы тяжести

В безвоздушном пространстве снаряд, выпущенный из пушки под некоторым углом к горизонту, будет двигаться по параболе под действием силы тяжести. Если в какой-либо момент времени снаряд разорвется на мелкие осколки, то эти осколки под действием внутренних сил будут разлетаться в разные стороны. Однако центр масс осколков и газов, образовавшихся при взрыве, будет продолжать свое движение по параболической траектории, как если бы никакого взрыва не было. Действительно, результирующая внешняя сила, действующая на продукты распада, равна силе тяжести, действовавшей на неразорвавшийся снаряд.

При взрыве праздничной ракеты центр масс продуктов распада в течение некоторого времени продолжает двигаться по траектории, по которой двигалась бы ракета, если бы взрыва не произошло

2.9. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ.
ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ

Галилео Галилей (Galileo Galilei), 1564–1642

Галилео Галилей – великий итальянский физик, механик и астроном. Родился в Пизе в 1564 г. в тот самый день, когда умер Микеланджело. Галилей по праву считается одним из основоположников точного естествознания. Ряд открытий Галилея и некоторые его взгляды имели непосредственное отношение к движению небесных тел. В 1632 г. вышла его книга «Диалог о двух главнейших системах мира – Птолемеевой и Коперниковой», в которой Галилей в доступной форме изложил свои взгляды на систему мира Коперника. А годом позже Галилей был вызван на суд римской инквизиции, и там коленопреклоненный был вынужден поклясться, что отрекается от идеи о неподвижном Солнце и движущейся Земле. Он был взят под домашний арест. Однако Галилей не был сломлен. Страдая от болезней и переживаний, он все же нашел в себе силы и мужество, чтобы написать новую книгу «Беседы и математические доказательства, касающиеся двух новых отраслей наук». Это был самый значительный труд Галилея, в котором сконцентрировались плоды всех его научных поисков. Эта книга была издана в Лейдене в 1636 г.

Заслуга Галилея заключалась в том, что он опроверг ошибочное положение динамики Аристотеля и заложил основы современной механики, выдвинул идею об относительности движения, установил законы инерции, свободного падения и движения тел по наклонной плоскости. Галилей первым направил телескоп в небо, открыл горы на Луне, четыре спутника Юпитера, фазы у Венеры и пятна на Солнце.

Прожив 78 лет, совершенно потеряв зрение, Галилей умер 8 января 1642 г., того самого года, в котором на Земле суждено было появиться Ньютону.

Физики любой эпохи будут с благодарностью и уважением вспоминать Галилея, указавшего на то, что новые идеи надо искать «в великой книге – природе», опираясь только на факты.

В 1632 г. в книге «Диалог о двух главнейших системах мира – Птолемеевой и Коперниковой» Галилей обосновал принцип относительности, ставший одним из первых основных принципов физики. Согласно этому принципу все ИСО по своим механическим свойствам эквивалентны друг другу. Это значит, что никакими механическими опытами, проводимыми внутри данной ИСО, нельзя установить, покоится эта система или движется равномерно и прямолинейно. Этот принцип является обобщением опыта и подтверждается всем многообразием приложений механики Ньютона к движению тел, скорости которых значительно меньше скорости света.

Все сказанное достаточно ясно свидетельствует об исключительности свойств ИСО, в силу чего именно эти системы должны, как правило, использоваться для изучения механических явлений.

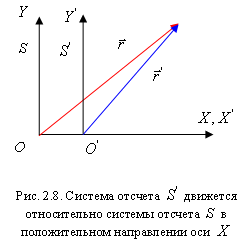
Найдем формулы преобразования координат при переходе от одной ИСО к другой. Допустим, что система отсчета S инерциальна. Рассмотрим вторую систему отсчета S', движущуюся относительно первой поступательно с постоянной скоростью (рис. 2.8). Свяжем с каждой системой отсчета декартову систему координат. Пусть известно движение точки в одной из этих систем, например, в системе S, то есть известна зависимость координат точки от времени. Как найти движение той же точки в системе отсчета S'? Задача сводится к нахождению формул, выражающих координаты движущейся точки в системе отсчета S' через ее координаты в системе отсчета S в один и тот же момент времени. Начало координат и направление координатных осей можно выбрать произвольно как в системе отсчета S, так и в системе отсчета S'. Для простоты можно принять, что координатные оси 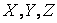системы S соответственно параллельны координатным осям 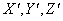системы S' и что в начальный момент 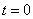начало системы координат, связанной с системой отсчета S, совпадает с началом системы координат, связанной с системой отсчета S'. Кроме того, предположим, что скорость параллельна оси . 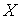При этих условиях ось 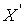будет все время совпадать с осью .

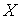Пусть в момент времени 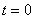движущаяся точка находится в положении M. За время 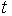начало координат S' переходит из точки О в положение 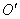, причем, так как 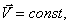то

,

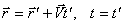(2.12)

где 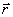и 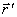– радиус-векторы движущейся точки соответственно в системах отсчета S и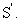

Спроецируем соотношение (2.12) на оси координат:

(2.13)

Формулы обратного преобразования имеют вид

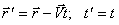
или в координатной форме

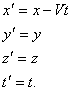
(2.14)

Формулы (2.12–2.14) и дают решение поставленной задачи. Они называются преобразованиями Галилея. Мы присоединили к формулам преобразования координат дополнительное выражение 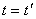, чтобы явно отметить, что время в механике Ньютона считается абсолютным (то есть не меняется при переходе от одной системы отсчета к другой) и поэтому не преобразуется.

С точки зрения «здравого смысла» преобразования Галилея кажутся очевидными. Однако в основе вывода лежит предположение механики Ньютона об абсолютности длин и промежутков времени. Абсолютность времени явно отмечена в уравнении 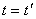, при выводе остальных формул использовалось предположение об абсолютности длин. Действительно, формулы (2.12–2.14) были бы очевидными, есл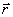и и 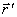измерялись бы в одной системе отсчета. Мы же измеряем их в разных системах отсчета. По этой причине без предположения об абсолютности расстояний и промежутков времени нельзя обойтись. Релятивистская физика отказалась от такой абсолютности.

Чтобы получить формулы сложения скоростей в нерелятивистской механике, возьмем производную по времени от (2.12):

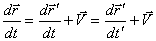
или

,

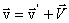(2.15)

где 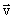– скорость точки в системе отсчета S, а 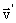– в системе отсчета 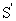. Эта формула выражает закон сложения скоростей в классической механике.

Возьмем производную по времени от (2.15), тогда получим

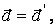
(2.16)

где 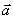– ускорение точки в системе отсчета S, 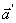– в системе отсчета 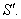Таким образом, ускорение точки в обеих системах отсчета одинаково. Говорят, что ускорение инвариантно относительно преобразований Галилея.

По определению ИСО свободная материальная точка движется в системе отсчета S без ускорения. Формула (2.16) показывает, что движение данной материальной точки в системе отсчета 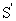будет также неускоренным. Следовательно, 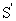– также инерциальная система отсчета. Таким образом, система отсчета, движущаяся относительно инерциальной системы отсчета прямолинейно и равномерно, также является инерциальной системой. Следовательно, если существует хотя бы одна ИСО, то существует и бесконечное множество ИСО, движущихся относительно друг друга равномерно и прямолинейно.

Сила в классической механике может зависеть от разностей координат, разностей скоростей взаимодействующих точек и от времени. Поэтому, как видно из преобразований Галилея, она не меняется при переходе от одной системы отсчета к другой. Отсюда следует, что уравнение, выражающее второй закон Ньютона, остается неизменным при переходе от одной ИСО к другой. Такие уравнения называются инвариантными. Таким образом, уравнения механики Ньютона инвариантны относительно преобразований Галилея. Это утверждение и составляет содержание принципа относительности Галилея. Равноправие ИСО дает возможность в каждом конкретном случае подбирать систему отсчета, наиболее удобную для решения рассматриваемой задачи.

Итак, принцип относительности Галилея выражает полное равноправие всех ИСО. Однако означает ли это, что одно и то же движение выглядит одинаково во всех ИСО? Конечно, нет! Движение тела, свалившегося с полки равномерно движущегося вагона, является прямолинейным, если его рассматривать относительно вагона. Но то же самое движение происходит по параболе в системе отсчета, связанной с полотном железной дороги, хотя законы механики Ньютона одинаковы в обеих системах отсчета. Движения выглядят по-разному, так как для описания движения к уравнению движения необходимо добавить начальные условия, то есть задать начальное положение тела и его начальную скорость, а они будут различными в разных системах отсчета.

Date: 2015-09-17; view: 723; Нарушение авторских прав