Роль начальных условий

Векторное уравнение движения материальной точки можно записать в координатной форме:

, , .

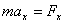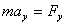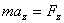(2.6)

Эти три скалярных уравнения, эквивалентные одному векторному уравнению, являются дифференциальными, то есть в них входят вторые производные от координат по времени 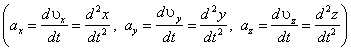, поэтому их недостаточно для однозначного описания движения материальной точки. Для однозначного описания движения точки к уравнениям движения надо присоединить дополнительные данные, определяющие значения шести числовых постоянных, получающихся при решении уравнений (2.6), в которые входят вторые производные. В качестве таковых обычно берут значения pадиус-вектора и скорости в момент времени 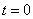. Эти значения называются начальными условиями.

Поясним этот вопрос на примере движения материальной точки под действием силы тяжести 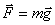. Уравнение движения в этом случае запишется следующим образом:

.

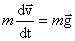(2.7)

Это уравнение эквивалентно двум уравнениям:

, .

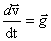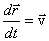Легко проверить, что этим уравнения удовлетворяют следующие решения:

, ,

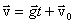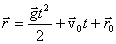(2.8)

где 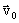и 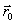– произвольные постоянные векторы. Убедиться в этом можно, если взять производные от 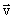и 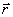по времени. Решение (2.8) называется общим решением уравнения (2.7). Общее решение – это, в сущности, не одно решение, а целое семейство решений, зависящих от двух произвольных векторных постоянных 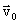и 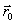. Придавая этим постоянным какие-либо конкретные значения, мы выделяем из этого семейства определенное частное решение. Постоянная 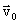– начальная скорость движущейся точки, 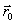– ее радиус-вектор в начальный момент времени. Величины 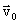и 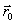определяются начальными условиями. В зависимости от их значений движения могут сильно отличаться друг от друга: тело может двигаться вверх или вниз по прямой линии, может описывать параболу, достигая или не достигая ее вершины. Получается довольно разнообразный класс движений. Заслуга Ньютона и состоит в том, что он подметил, что все многообразие движений может быть описано единой формулой, не содержащей никаких произвольных постоянных, если от положений и скоростей материальной точки перейти к ее ускорению.

Date: 2015-09-17; view: 642; Нарушение авторских прав